
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
分析 方法一:由抛物线的焦点弦公式求得丨AF丨+丨BF丨=x1+x2+2,由丨AD丨=丨BD丨,利用两点之间的距离公式即可求得x1+x2=6,即可求得|AF|+|BF|;
方法二:由抛物线的焦点弦公式求得丨AF丨+丨BF丨=x1+x2+2,利用点差法求得直线AB的斜率,即可求得直线AB的中垂线方程,将D代入即可求得x1+x2,即可求得|AF|+|BF|.
解答 解:方法一:抛物线y2=4x的焦点F(1,0),
A(x1,y1),B(x2,y2),y12=4x1,y22=4x2,
则丨AF丨+丨BF丨=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$=x1+x2+2,
由线段AB的中垂线交x轴于点D(5,0),则丨AD丨=丨BD丨,
(x1-5)2+y12=(x2-5)2+y22,整理得:(x1+x2-10)(x1-x2)=y22-y12=4(x2-x1),
x1+x2-10=-4,x1+x2=6,
∴|AF|+|BF|=8.
故选C.
方法二:抛物线y2=4x的焦点F(1,0),
A(x1,y1),B(x2,y2),y12=4x1,y22=4x2,
则丨AF丨+丨BF丨=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$=x1+x2+2,
则AB的中点坐标为:($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),
由$\left\{\begin{array}{l}{{y}_{1}^{2}=4{x}_{1}}\\{{y}_{2}^{2}=4{x}_{2}}\end{array}\right.$,整理得:(y2-y1)(y2+y1)=4(x2-x1),
直线AB的斜率k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{4}{{y}_{1}+{y}_{2}}$,则直线AB的中垂线的斜率-$\frac{{y}_{1}+{y}_{2}}{4}$,
中垂线方程y-$\frac{{y}_{1}+{y}_{2}}{2}$=-$\frac{{y}_{1}+{y}_{2}}{4}$(x-$\frac{{x}_{1}+{x}_{2}}{2}$),
将D(5,0),代入,解得:x1+x2=6,
∴|AF|+|BF|=8.
故选C.
点评 本题考查抛物线的简单几何性质,直线与抛物线的位置关系,抛物线的焦点弦公式,考查点差法的应用,直线的斜率公式,考查计算能力,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | 7 | C. | 15 | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
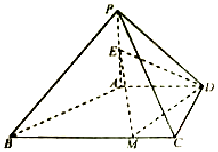 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平面ABC⊥平面ACD | |
| B. | 四面体D-ABC的体积是$\frac{16}{3}\sqrt{6}$ | |
| C. | 二面角A-BC-D的正切值是$\frac{{\sqrt{42}}}{5}$ | |
| D. | BC与平面ACD所成角的正弦值是$\frac{{\sqrt{21}}}{14}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com