
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 把z1=1+2i,z2=1-i代入$\frac{z_1}{z_2^2}$,利用复数代数形式的乘除运算化简,求出$\frac{z_1}{z_2^2}$得坐标得答案.
解答 解:∵z1=1+2i,z2=1-i,则复数$\frac{z_1}{z_2^2}$=$\frac{1+2i}{(1-i)^{2}}=\frac{1+2i}{-2i}=\frac{(1+2i)•i}{-2{i}^{2}}=\frac{-2+i}{2}=-1+\frac{i}{2}$.
∴复数$\frac{z_1}{z_2^2}$在复平面内对应点的坐标为(-1,$\frac{1}{2}$),位于第二象限.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 9 | C. | 1 | D. | -$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
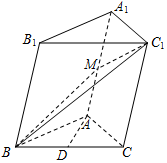 在斜三棱柱ABC-A1B1C1中,AB=AC,平面BB1C1C⊥底面ABC,点M、D分别是线段AA1、BC的中点.
在斜三棱柱ABC-A1B1C1中,AB=AC,平面BB1C1C⊥底面ABC,点M、D分别是线段AA1、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 |
| 年利润/十万元 | 1 | 6 | 15 | 28 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
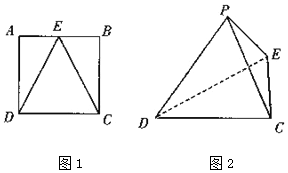 如图1,2,E是正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.
如图1,2,E是正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com