
| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
分析 首先由已知求出α,α+β的其它三角函数值,然后由β=α+β-α,求出β的三角函数值,再借助于倍角公式求值.
解答 解:由已知α为锐角,且$tanα=\frac{1}{7}$,得到sinα=$\frac{\sqrt{2}}{10}$,cosα=$\frac{7\sqrt{2}}{10}$,
由$cos({α+β})=\frac{{2\sqrt{5}}}{5}$,得到sin(α+β)=$\frac{\sqrt{5}}{5}$,
所以cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=$\frac{2\sqrt{5}}{5}×\frac{7\sqrt{2}}{10}+\frac{\sqrt{5}}{5}×\frac{\sqrt{2}}{10}=\frac{15\sqrt{10}}{50}=\frac{3\sqrt{10}}{10}$,
所以cos2β=2cos2β-1=$2×\frac{9}{10}-1=\frac{4}{5}$;
故选C.
点评 本题考查了三角函数式的化简求值;熟练运用两角和与差的三角函数以及角的等价变化、倍角公式是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
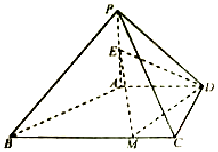 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,6) | B. | (-∞,-2)∪(3,6) | C. | (3,4) | D. | (-∞,-2)∪(3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平面ABC⊥平面ACD | |
| B. | 四面体D-ABC的体积是$\frac{16}{3}\sqrt{6}$ | |
| C. | 二面角A-BC-D的正切值是$\frac{{\sqrt{42}}}{5}$ | |
| D. | BC与平面ACD所成角的正弦值是$\frac{{\sqrt{21}}}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com