
分析 先根据题意求出过点Pn,Pn+1的直线方程为y-$\frac{2}{n}$=-$\frac{2}{n(n+1)}$(x-n),分别令x=0,y=0,表示出bn=4+$\frac{1}{n}$-$\frac{1}{n+1}$,再分组求和即可.
解答 解:由题意可得Pn的坐标(n,$\frac{2}{n}$),Pn+1的坐标为(n+1,$\frac{2}{n+1}$),
则过点Pn,Pn+1的直线方程为y-$\frac{2}{n}$=-$\frac{2}{n(n+1)}$(x-n),
令x=0,解得y=$\frac{2}{n}$+$\frac{2}{n+1}$,
令y=0,解得x=2n+1,
∴bn=$\frac{1}{2}$•($\frac{2}{n}$+$\frac{2}{n+1}$)(2n+1)=2+$\frac{n+1}{n}$+$\frac{n}{n+1}$=4+$\frac{1}{n}$-$\frac{1}{n+1}$
∴Sn=4n+1-$\frac{1}{2}$+$\frac{1}{2}$$-\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=4n+1-$\frac{1}{n+1}$=4n+$\frac{n}{n+1}$,
∴S5=20+$\frac{5}{6}$=$\frac{125}{6}$,
故答案为:$\frac{125}{6}$
点评 本题考查了数列在解析几何中的应用,以及直线方程的求法和三角形的面积公式,考查了学生的分析问题,解决问题的能力,属于中档题


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
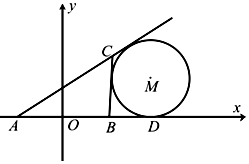 如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
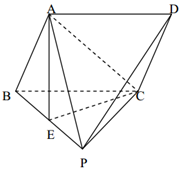 如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.
如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ①② |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
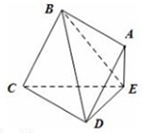 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com