
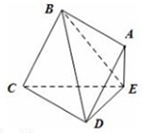
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.分析 (Ⅰ)推导出AE⊥CD,AD⊥CD,从而CD⊥平面ADE,由此能证明平面ABCD⊥平面ADE.
(Ⅱ)推导出BA⊥平面ADE,AE⊥DE,由此利用VB-ADE=VA-BDE,能求出AE的长.
解答 证明:(Ⅰ)∵AE⊥平面CDE,CD?平面CDE,
∴AE⊥CD,
∵AD⊥CD,∴CD⊥平面ADE,
又CD?面ABCD,∴平面ABCD⊥平面ADE.
解:(Ⅱ)∵平面ABCD⊥平面ADE,且BA⊥DA,
∴BA⊥平面ADE,
∵AE⊥平面CDE,∴AE⊥DE,
设AE=x,DA=2,得DE=$\sqrt{4-{x}^{2}}$,
∴VB-ADE=$\frac{1}{3}×\frac{1}{2}x\sqrt{4-{x}^{2}}$×2=$\frac{1}{3}x\sqrt{4-{x}^{2}}$,
∵VB-ADE=VA-BDE=$\frac{\sqrt{3}}{3}$,∴$x\sqrt{4-{x}^{2}}$=$\sqrt{3}$,
解得x=1或x=$\sqrt{3}$.
∴AE=1或AE=$\sqrt{3}$.
点评 本题考查面面垂直的证明,考查线段长的求法,考查推理论证能力、运算求解能力、空间思维能力,考查函数与方程思想、化归转化思想、数形结合思想,是中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平面ABC⊥平面ACD | |
| B. | 四面体D-ABC的体积是$\frac{16}{3}\sqrt{6}$ | |
| C. | 二面角A-BC-D的正切值是$\frac{{\sqrt{42}}}{5}$ | |
| D. | BC与平面ACD所成角的正弦值是$\frac{{\sqrt{21}}}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
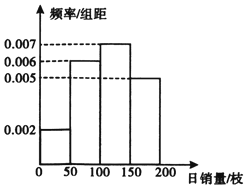 某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.
某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com