
分析 (1)求出曲线C1:x2+y2=1.直线l的参数方程代入,得t2+2t(cosα+sinα)+1=0,由此能证明|MA|•|MB|为定值.
(2)将曲线C1上的任意点(x,y)伸缩变换后得C2:$\frac{x^2}{3}+{y^2}=1$.由此能求出曲线C2的内接矩形ABCD周长的最大值.
解答 证明:(1)∵曲线C1:p=1,∴曲线C1:x2+y2=1.
联立$\left\{\begin{array}{l}x=1+tcosα\\ y=1+tsinα\\{x^2}+{y^2}=1\end{array}\right.$,得t2+2t(cosα+sinα)+1=0,
∴|MA|•|MB|=|t1t2|=1.
解:(2)将曲线C1上的任意点(x,y)作伸缩变换$\left\{\begin{array}{l}x'=\sqrt{3x}\\ y'=y\end{array}\right.$,
伸缩变换后得C2:$\frac{x^2}{3}+{y^2}=1$.
其参数方程为:$\left\{\begin{array}{l}x=\sqrt{3}cosθ\\ y=sinθ\end{array}\right.$.
不妨设点A(m,n)在第一象限,
由对称性知:周长为$4({m+n})=4({\sqrt{3}cosθ+sinθ})$=$8sin({θ+\frac{π}{3}})≤8$,($θ=\frac{π}{6}$时取等号),
∴曲线C2的内接矩形ABCD周长的最大值为8.
点评 本题考查两线段乘积为定值的证明,考查曲线内接矩形周长的最大值的求法,考查参数方程、直角坐标方程、极坐标方程互化公式的应用,考查运算求解能力、转化化归思想,是中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ①② |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
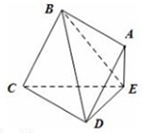 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
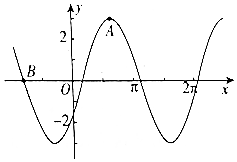 已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$)..
已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$)..查看答案和解析>>
科目:高中数学 来源: 题型:填空题
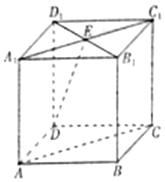 如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.
如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,2] | C. | [-1,4] | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com