
 已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$)..
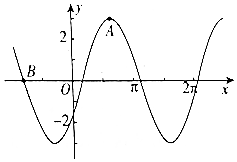
已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).. 分析 首先通过A为最高点得到M,然后根据A,B的水平距离求得周期,通过图象经过的点求φ
解答 解:由已知图象得到M=3,$\frac{3}{4}T=2+\frac{5}{2}=\frac{9}{2}$,所以T=6=$\frac{2π}{ω}$,所以ω=$\frac{π}{3}$,又图象经过B(-$\frac{5}{2}$,0),所以sin(-$\frac{5π}{6}$+φ)=0,|φ|<$\frac{π}{2}$),所以φ=-$\frac{π}{6}$,
所以f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).
故答案为:3sin($\frac{π}{3}$x-$\frac{π}{6}$).
点评 本题考查了由y=Asin(ωx+φ)的部分图象确定其解析式部分;注意最高点、最低点、零点等关键点.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平面ABC⊥平面ACD | |
| B. | 四面体D-ABC的体积是$\frac{16}{3}\sqrt{6}$ | |
| C. | 二面角A-BC-D的正切值是$\frac{{\sqrt{42}}}{5}$ | |
| D. | BC与平面ACD所成角的正弦值是$\frac{{\sqrt{21}}}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
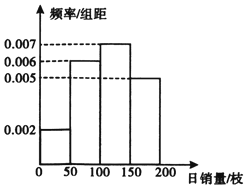 某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.
某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| B. | 奇函数,在(-∞,0)上递减,在(0,+∞)上递减 | |
| C. | 偶函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| D. | 偶函数,在(-∞,0)上递减,在(0,+∞)上递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com