
| A. | 奇函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| B. | 奇函数,在(-∞,0)上递减,在(0,+∞)上递减 | |
| C. | 偶函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| D. | 偶函数,在(-∞,0)上递减,在(0,+∞)上递减 |
分析 根据题意,写出函数g(x)的解析式,设x>0,则-x<0,分析可得g(-x)=-g(x),可得g(x)为奇函数;由x>0时g(x)的解析式,对其求导可得g′(x)=-2•$\frac{1}{{x}^{3}}$=$\frac{-2}{{x}^{3}}$<0,可得函数g(x)在区间(0,+∞)上递减,结合单调性可得其在(-∞,0)上也递减,综合可得答案.
解答 解:根据题意,$g(x)=\frac{f(x)}{x^2}$=$\left\{\begin{array}{l}{\frac{1}{{x}^{2}},x>0}\\{-\frac{1}{{x}^{2}},x<0}\end{array}\right.$,
设x>0,则-x<0,g(-x)=-$\frac{1}{(-x)^{2}}$=-$\frac{1}{{x}^{2}}$=-g(x),故g(x)为奇函数;
当x>0时,g(x)=$\frac{1}{{x}^{2}}$=x-2,
g′(x)=-2•$\frac{1}{{x}^{3}}$=$\frac{-2}{{x}^{3}}$<0,
即g(x)在区间(0,+∞)上递减,
又由函数g(x)为奇函数,则在(-∞,0)上也递减,
故选:B.
点评 本题考查函数的奇偶性单调性的判定,涉及分段函数的应用,关键是写出g(x)的解析式.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | $(-1,-\frac{1}{2})$ | C. | $(-2,-\frac{1}{2})$ | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
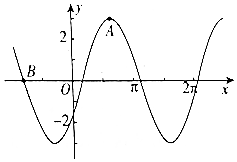 已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$)..
已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$)..查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,2] | C. | [-1,4] | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com