
分析 (Ⅰ)由曲线C1的参数方程求出曲线C1的直角坐标方程,由曲线C2的极坐标方程求出曲线C2的直角坐标方程,由此能求出结果.
(Ⅱ)联立曲线C1和C2的直角坐标方程,得3y2+2y-4=0,由此利用图形对称性知公共点的个数为2.
(Ⅲ)利用椭圆参数方程的性质能求出a+2b的取值范围.
解答 (本小题满分10分)
解:(Ⅰ)∵曲线C1的参数方程为$\left\{\begin{array}{l}x=2cost\\ y=sint\end{array}\right.$(t为参数),
∴由题设知曲线C1的直角坐标方程是$\frac{x^2}{4}+{y^2}=1$.
∴曲线C1表示以$(±\sqrt{3},0)$为焦点,中心为原点的椭圆.…(3分)
∵曲线C2:ρ=2sinθ,
∴曲线C2的直角坐标方程是x2+y2-2y=0.
∴曲线C2表示以(0,1)为圆心,半径是1的圆.…(5分)
(Ⅱ)联立曲线C1和C2的直角坐标方程,得$\left\{\begin{array}{l}{x^2}+4{y^2}=4\\{x^2}+{y^2}-2y=0\end{array}\right.$.
消去x,得3y2+2y-4=0,
解得$y=\frac{{\sqrt{13}-1}}{3}$或$y=\frac{{-\sqrt{13}-1}}{3}(舍)$.
由图形对称性知公共点的个数为2.…(8分)
(Ⅲ)a+2b的取值范围是$[-2\sqrt{2},2\sqrt{2}]$. …(10分)
点评 本题考查曲线的直角坐标方程的求法,考查两曲线交点个数的求法,考查代数式的取值范围的求法,考查化归转化思想、函数与方程思想,考查推理论证能力、运算求解能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 奇函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| B. | 奇函数,在(-∞,0)上递减,在(0,+∞)上递减 | |
| C. | 偶函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| D. | 偶函数,在(-∞,0)上递减,在(0,+∞)上递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
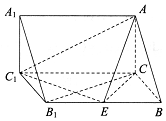 如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.
如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
| 男 | 1 | 2 | 3 | 6 | 8 |
| 女 | 0 | 2 | 10 | 6 | 2 |
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
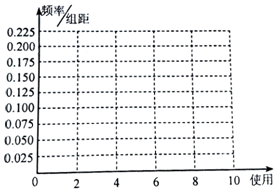 共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:| 使用时间 | [0,2] | (2,4] | (4,6] | (6,8] | (8,10] |
| 人数 | 10 | 40 | 25 | 20 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com