
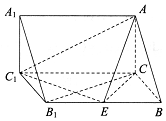
 如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.
如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.分析 (1)证明B1C⊥BC.AC⊥B1C,推出B1C⊥平面ABC,即可证明B1C⊥AB.
(2)以C为原点,建立空间直角坐标系C-xyz,求出相关点的坐标,求出平面AEC1的一个法向量,平面EC1C的一个法向量利用二面角的平面角转化求解即可.
解答 解:(1)证明:在△BCB1中,BC=1,BB1=2,∠B1BC=60°,
则${B_1}C=\sqrt{{1^2}+{2^2}-2×1×2•cos{{60}°}}=\sqrt{3}$,
于是$B{C^2}+{B_1}{C^2}=BB_1^2$,故B1C⊥BC.
所以AC⊥平面BCC1B1,于是AC⊥B1C,又BC∩AC=C,
故B1C⊥平面ABC,所以B1C⊥AB.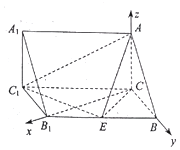
(2)如图,以C为原点,建立空间直角坐标系C-xyz,则$C({0,0,0}),{B_1}({\sqrt{3},0,0}),B({0,1,0}),A({0,0,1})$,
由$\overrightarrow{B{B_1}}=\overrightarrow{C{C_1}}$,得${C_1}({\sqrt{3},-1,0})$,设$\overrightarrow{BE}=λ\overrightarrow{B{B_1}}({0≤λ≤1})$,
则$E({\sqrt{3}λ,1-λ,0})$,于是$\overrightarrow{AE}=({\sqrt{3}λ,1-λ,-1}),\overrightarrow{A{C_1}}=({\sqrt{3},-1,-1})$,
求得平面AEC1的一个法向量为$\overrightarrow n=({λ-2,\sqrt{3}λ-\sqrt{3},-\sqrt{3}})$,
取平面EC1C的一个法向量为$\overrightarrow m=({0,0,1})$,又二面角A-EC1-C为45°,
则$cos{45°}=\frac{{|{\overrightarrow m•\overrightarrow n}|}}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}=\frac{{\sqrt{3}}}{{\sqrt{{{({λ-2})}^2}+3{{({λ-1})}^2}+3}}}=\frac{{\sqrt{3}}}{{\sqrt{4{λ^2}-10λ+10}}}$,
解得$λ=\frac{1}{2}$或λ=2(舍),
所以$\frac{BE}{{B{B_1}}}$的值为$\frac{1}{2}$.
点评 本题考查空间向量的数量积的应用,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | aial≤ajak | B. | aial≥ajak | C. | SiSl<SjSk | D. | SiSl≥SjSk |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com