
分析 (1)运用数列的递推式可得n≥2时,an+1=2an,再由等比数列的通项公式和求和公式,即可得到所求数列的通项公式;
(2)求得cn=nbn+$\frac{n+1}{{2}^{n}}$=2n-$\frac{n}{{2}^{n-1}}$+$\frac{n+1}{{2}^{n}}$,运用数列的求和方法:分组求和和裂项相消求和,即可得到所求和,即可得证.
解答 解:(1)由Sn+1=3Sn-2Sn-1(n≥2),可得Sn+1-Sn=2(Sn-Sn-1),
即为n≥2时,an+1=2an,
a1=$\frac{1}{2}$a2≠0,可得$\frac{{a}_{n+1}}{{a}_{n}}$=2,即数列{an}(n∈N*)是以2为公比的等比数列,
故an=a1•2n-1,Sn=$\frac{{a}_{1}(1-{2}^{n})}{1-2}$=a1•(2n-1),
则bn=$\frac{{S}_{n}}{{a}_{n}}$=$\frac{{2}^{n}-1}{{2}^{n-1}}$.
(2)证明:cn=nbn+$\frac{n+1}{{2}^{n}}$=2n-$\frac{n}{{2}^{n-1}}$+$\frac{n+1}{{2}^{n}}$,
则T10=2(1+2+…+10)-$\frac{1}{{2}^{0}}$+$\frac{2}{{2}^{1}}$-$\frac{2}{{2}^{1}}$+$\frac{3}{{2}^{2}}$+…-$\frac{10}{{2}^{9}}$+$\frac{11}{{2}^{10}}$
=2×$\frac{1}{2}$×10×11-1+$\frac{11}{{2}^{10}}$=109+$\frac{11}{{2}^{10}}$>109.
点评 本题考查数列的通项公式的求法,注意运用数列递推式,考查等比数列的通项公式和求和公式的运用,以及数列的求和方法:分组求和与裂项相消求和,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
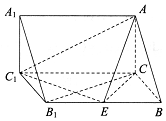 如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.
如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
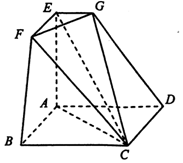 如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.
如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:
某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:| x(元) | 25 | 30 | 38 | 45 | 52 |
| 销售y(万册) | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,总有(x+1)ex≤1 | B. | ?x≤0,总有(x+1)ex≤1 | ||
| C. | ?x0≤0,总有(x0+1)${e}^{{x}_{0}}$≤1 | D. | ?x0>0,使得(x0+1)${e}^{{x}_{0}}$≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com