
| 步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
| 男 | 1 | 2 | 3 | 6 | 8 |
| 女 | 0 | 2 | 10 | 6 | 2 |
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (Ⅰ)根据题意完成下面的2×2列联表,求出K2=$\frac{40}{11}<3.841$,由此能没有95%以上的把握认为二者有关.
(Ⅱ)由题知,小王的微信好友中任选一人,其每日走路步数不超过5000步的概率为$\frac{1}{8}$,超过10000步的概率为$\frac{1}{4}$,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 解:(Ⅰ)根据题意完成下面的2×2列联表:
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| ξ | 0 | 1 | 2 |
| P | $\frac{29}{64}$ | $\frac{30}{64}$ | $\frac{5}{64}$ |
点评 本题考查独立检验,考查离散型随机变量的分布列和数学期望的求法,考查推理论证能力、运算求解能力,考查化归转化思想、函数与方程思想,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | aial≤ajak | B. | aial≥ajak | C. | SiSl<SjSk | D. | SiSl≥SjSk |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1587 | B. | 0.3413 | C. | 0.1826 | D. | 0.5000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
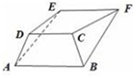 我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )
我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )| A. | 约84立方尺 | B. | 约为105立方尺 | C. | 恰为84立方尺 | D. | 恰为105立方尺 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com