
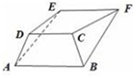
 我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )
我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )| A. | 约84立方尺 | B. | 约为105立方尺 | C. | 恰为84立方尺 | D. | 恰为105立方尺 |
分析 五面体EF-ABCD中,四边形ADEF,ABCD,EFBC均为等腰梯形,EF∥AD∥BC,△ABF,△CDE均为直角三角形,连接BE,BD,AE,得到三个三棱锥,设三棱锥BAEF的体积为V1,三棱锥BAED的体积为V2,三棱锥BDEC的体积为V3,由此能求出五面体的体积.
解答 解:本题是求规则形状的五面体的体积,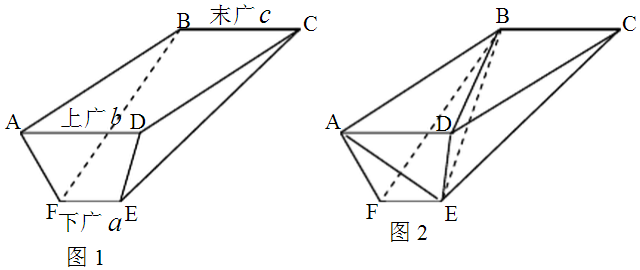
如图,五面体EF-ABCD中,四边形ADEF,ABCD,EFBC均为等腰梯形,
EF∥AD∥BC,△ABF,△CDE均为直角三角形,
AB⊥AF,CD⊥DE,设下广EF=a,上广AD=b,末广BC=c,
高EF到平面ABCD的距离为h,AD与BC的距离为l,
连接BE,BD,AE,如图2,
得到三个三棱锥,设三棱锥BAEF的体积为V1,三棱锥BAED的体积为V2,三棱锥BDEC的体积为V3,
则${V}_{3}=\frac{1}{6}clh$,${V}_{2}=\frac{1}{6}blh$,$\frac{{V}_{1}}{{V}_{2}}$=$\frac{b}{a}$,${V}_{1}=\frac{a}{b}{V}_{2}$,
∴${V}_{1}=\frac{a}{b}{{V}_{2}}^{\;}$=$\frac{1}{6}alh$,
∴五面体的体积:
V=V1+V2+V3=$\frac{1}{6}$(a+b+c)×h×l=$\frac{1}{6}$(6+10+8)×3×7=84(立方尺).
故选:C.
点评 本题考查几何体的体积及直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查考查推理论证能力、运算求解能力、空间想象能力,考查化归转化思想,数形结合思想,是中档题.


科目:高中数学 来源: 题型:解答题
| 步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
| 男 | 1 | 2 | 3 | 6 | 8 |
| 女 | 0 | 2 | 10 | 6 | 2 |
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
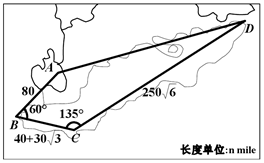 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-2x-4 | B. | x2+x-1 | C. | x2+2x | D. | x2-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com