
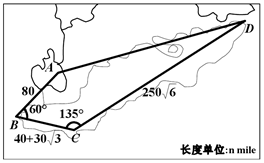
 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$. 分析 求出AD,可得∠DAC=90°,即可得出结论.
解答 解:由题意,AC=$\sqrt{6400+1600+2700+2400\sqrt{3}-2×80×(40+30\sqrt{3})×\frac{1}{2}}$=50$\sqrt{3}$nmile,
60min后,轮船到达D′,AD′=50×1=50nmile
∵$\frac{50\sqrt{3}}{80}$=$\frac{50\sqrt{3}}{\frac{\sqrt{3}}{2}}$∴sin∠ACB=$\frac{4}{5}$,
∴cos∠ACD=cos(135°-∠ACB)=$\frac{\sqrt{2}}{10}$,
∴AD=$\sqrt{7500+62500×6-2×50\sqrt{3}×250\sqrt{6}×\frac{\sqrt{2}}{10}}$=350$\sqrt{3}$,
∴cos∠DAC=$\frac{7500+122500×3-62500×6}{2×50\sqrt{3}×350\sqrt{3}}$=0,∴∠DAC=90°,
∴CD′=$\sqrt{2500+7500}$=100,∴∠AD′C=60°,
∴sinθ=sin(75°-60°)=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$,
故答案为$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
点评 本题考查正弦、余弦定理的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1587 | B. | 0.3413 | C. | 0.1826 | D. | 0.5000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z=-3+i | B. | $\overline z=3-i$ | C. | z=1-3i | D. | $\overline z=-1+3i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
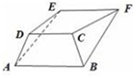 我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )
我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )| A. | 约84立方尺 | B. | 约为105立方尺 | C. | 恰为84立方尺 | D. | 恰为105立方尺 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com