
分析 运用向量数量积的性质,主要是向量的平方即为模的平方,以及向量垂直的条件:数量积为0,解方程即可得到所求值.
解答 解:|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且$\overrightarrow a+2\overrightarrow b$与$λ\overrightarrow a-\overrightarrow b$垂直,
可得($\overrightarrow a+2\overrightarrow b$)•($λ\overrightarrow a-\overrightarrow b$)=0,
可得λ$\overrightarrow{a}$2-2$\overrightarrow{b}$2+(2λ-1)$\overrightarrow{a}$•$\overrightarrow{b}$=0,
由$\overrightarrow{a}$⊥$\overrightarrow{b}$,可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即有4λ-2×9+0=0,
解得λ=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查向量数量积的性质,主要是向量的平方即为模的平方,以及向量垂直的条件:数量积为0,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|1<x≤3} | C. | {x|1<x<3} | D. | {x|1≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
| 男 | 1 | 2 | 3 | 6 | 8 |
| 女 | 0 | 2 | 10 | 6 | 2 |
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
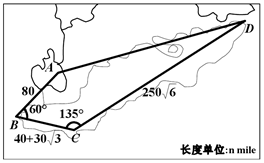 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com