
分析 (1)f(x)在点(a,mlna)处的切线为y=$\frac{m}{a}$(x-a)+mlna,h(x)在点(b,$\frac{1}{2}-\frac{1}{2b}$)处的切线为y=$\frac{1}{2{b}^{2}}$(x-b)+$\frac{1}{2}-\frac{1}{2b}$,由这两条切线重合知$\left\{\begin{array}{l}{\frac{m}{a}=\frac{1}{2{b}^{2}}}\\{-m+mlna=-\frac{1}{b}+\frac{1}{2}}\end{array}\right.$,问题即当m在什么范围内时,关于(a,b)的方程有唯一一组解,由此入手能求出m.
(2)问题等价于${f}_{1}(x)=x-a{e}^{x}-b$有两个不同的零点x1,x2,求证1+b-lna<x1+x2<-2lna,尝试使用构造函数的方法证明极值点偏移不等式.由此能证明$\frac{{{e^{1+b}}}}{a}$<x1x2<$\frac{1}{a^2}$.
解答 解:(1)f(x)在点(a,mlna)处的切线为y=$\frac{m}{a}$(x-a)+mlna,
h(x)在点(b,$\frac{1}{2}-\frac{1}{2b}$)处的切线为y=$\frac{1}{2{b}^{2}}$(x-b)+$\frac{1}{2}-\frac{1}{2b}$,
由这两条切线重合知$\left\{\begin{array}{l}{\frac{m}{a}=\frac{1}{2{b}^{2}}}\\{-m+mlna=-\frac{1}{b}+\frac{1}{2}}\end{array}\right.$,
问题即当m在什么范围内时,关于(a,b)的方程有唯一一组解,
∵a,b的值一一对应,如果在方程组中消去b,得到mlna+$\sqrt{\frac{2m}{a}}$-m-$\frac{1}{2}$=0,
此方程组对a>0有唯一解,不好计算;
如果在方程组中消去a,得到mln(2m)-m+2mlnb+$\frac{1}{b}-\frac{1}{2}$=0,
对b>0有唯一解,记左边为g(b),
则有g′(b)=$\frac{2mb-1}{{b}^{2}}$,
方程组有解时,有m>0,∴g(b)在(0,$\frac{1}{2m}$)上单调递减,在($\frac{1}{2m}$,+∞)上单调递增,
∴g(b)min=g($\frac{1}{2m}$)=m-$\frac{1}{2}$-mln(2m),
而当b→0与b→+∞时,均有g(b)→+∞,
∴当且仅当这个最小值等于0时,方程g(b)=0有唯一解.
最后解方程m-$\frac{1}{2}$-mln(2m)=0,
由题意知m=$\frac{1}{2}$是它的解,考虑h(m)=m-$\frac{1}{2}$-mln(2m),
有h′(m)=-ln(2m),∴h(m)在(0,$\frac{1}{2}$)上单调递增,在($\frac{1}{2}$,+∞)上单调递减,
∴$\frac{1}{2}$是h(m)=0的唯一解,
∴m=$\frac{1}{2}$.
(2)问题等价于${f}_{1}(x)=x-a{e}^{x}-b$有两个不同的零点x1,x2,
求证1+b-lna<x1+x2<-2lna,尝试使用构造函数的方法证明极值点偏移不等式.
右边不等式:∵${{f}_{1}}^{'}(x)=1-a{e}^{x}$,∴a>0,其极值点为x=-lna,
又∵函数f1(x)的二阶导函数${{f}_{1}}^{''}(x)=-a{e}^{x}$,
∴构造函数${g}_{1}(x)=\frac{1}{2}{{f}^{''}}_{1}(-lna)^{2}+{f}_{1}(-lna)$,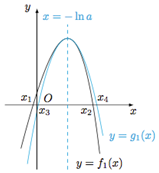
则h1(x)=f1(x)-g1(x)的二阶导数:
${{h}_{1}}^{''}(x)={{f}_{1}}^{''}(x)-{{f}_{1}}^{''}(-lna)=1-a{e}^{x}$,
∴在(-∞,-lna)上,${{h}_{1}}^{''}(x)>0$,
在(-lna,+∞)上,${{h}_{1}}^{''}(x)<0$,
结合${{h}_{1}}^{'}(-lna)=0$,在R上,${{h}_{1}}^{''}(x)≤0$,
结合h1(-lna)=0,在(-∞,-lna)上,h1(x)>0,在(-lna,+∞)上,h1(x)<0,如图,
∴二次函数${g}_{1}(x)=\frac{1}{2}{{f}_{1}}^{''}(-lna)•(x+lna)^{2}+{f}_{1}(-lna)$的零点x3,x4(x3<x4)满足:
x1<x3<x2<x4,
∴x1+x2<x3+x4=-2lna,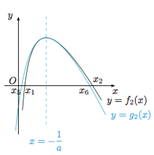
左边不等式:此时无法通过构造二次函数证明,
设f2(x)=lnx-(ax+b),
则其导函数${{f}_{2}}^{'}(x)=\frac{1}{x}-a$,∴其极大值点为x=$\frac{1}{a}$,
欲证明的不等式为:
lnx1+lnx2>1+b-lna,即${x}_{1}+{x}_{2}>\frac{1-b-lna}{a}$,
构造函数${g}_{2}(x)=-\frac{4}{ax+1}+2-lna-(ax+b)$,
其中g2(x)与f2(x) 在x=$\frac{1}{a}$处的函数值、导数值和二阶导函数值均相等,
则可以求得${g}_{2}(x)=-\frac{4}{ax+1}+2-lna-(ax+b)$,
此时h2(x)=f2(x)-g2(x)的导函数:
${{h}_{2}}^{'}(x)=\frac{1}{x}-\frac{4a}{(ax+1)^{2}}=\frac{(ax-1)^{2}}{x(ax+1{)^{2}}_{\;}}$≥0,
结合${h}_{2}(\frac{1}{a})=0$,得h2(x)在x=$\frac{1}{a}$的两侧异号,如图,
∵函数g2(x)的零点x5,x6(x5<x6)即方程$\frac{-{a}^{2}{x}^{2}+a(1-lna-b)-4}{ax+1}$=0的两根,
有${x}_{5}+{x}_{6}=\frac{1-b-lna}{a}$,
∴x5<x1<x6<x2,
∴${x}_{1}+{x}_{2}>{x}_{5}>{x}_{6}>\frac{1-b-lna}{a}$.
综上:$\frac{{{e^{1+b}}}}{a}$<x1x2<$\frac{1}{a^2}$.
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:填空题
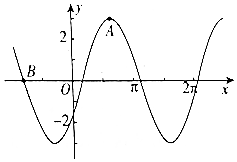 已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$)..
已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$)..查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 32 | C. | 48 | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com