
| A. | 0.1587 | B. | 0.3413 | C. | 0.1826 | D. | 0.5000 |
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
| 男 | 1 | 2 | 3 | 6 | 8 |
| 女 | 0 | 2 | 10 | 6 | 2 |
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:| 使用时间 | [0,2] | (2,4] | (4,6] | (6,8] | (8,10] |
| 人数 | 10 | 40 | 25 | 20 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
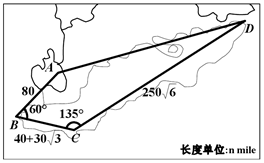 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com