
分析 (Ⅰ)求出f′(x)=2xlna+2xlnx+x,由f′(x)=0,得x=$\frac{1}{a\sqrt{e}}$,由此利用导数性质能求出函数y=f(x)的单调区间.
(Ⅱ)当0<x<$\frac{1}{e\sqrt{e}}$时,f(x)<0,ts2+t2>0,不存在S,使ts2+t2=f(s);当x≥$\frac{1}{e\sqrt{e}}$时,令h(x)=f(x),tx2-t2=x2lnex-tx2-t2,x∈[$\frac{1}{e\sqrt{e}}$,+∞),h′(x)=2xlnxex+x,tx=x(2lnx+3-2t),令M(x)=2lnx+3-2t,则M(x)在区间[$\frac{1}{e\sqrt{e}}$,+∞)内单调递增,由此能证明t>0时,存在唯一的s,使ts2+t2=f(s).
解答 解:(Ⅰ)∵函数f(x)=x2lnax(a>0),
∴函数f(x)的定义域为(0,+∞),
∵函数f(x)=x2lnax=x2lna+x2lnx,
∴f′(x)=2xlna+2xlnx+x,由f′(x)=0,得x=$\frac{1}{a\sqrt{e}}$,
由f′(x)<0,得0<x<$\frac{1}{a\sqrt{e}}$,由f′(x)>0,得x>$\frac{1}{a\sqrt{e}}$,
∴f(x)的减区间为(0,$\frac{1}{a\sqrt{e}}$),增区间为($\frac{1}{a\sqrt{e}}$,+∞).
证明:(Ⅱ)①当0<x<$\frac{1}{e\sqrt{e}}$时,f(x)<0,ts2+t2>0,此时,不存在S,使ts2+t2=f(s).
②当x≥$\frac{1}{e\sqrt{e}}$时,令h(x)=f(x),tx2-t2=x2lnex-tx2-t2,x∈[$\frac{1}{e\sqrt{e}}$,+∞),
h′(x)=2xlnxex+x,tx=x(2lnx+3-2t),
令M(x)=2lnx+3-2t,则M(x)在区间[$\frac{1}{e\sqrt{e}}$,+∞)内单调递增,
∵M($\frac{1}{e\sqrt{e}}$)=-2t<0,M(et)=3>0,
∴?x0∈($\frac{1}{e\sqrt{e}},{e}^{t}$),使M(x0)=0,
∴$x∈(\frac{1}{e\sqrt{e}},{x}_{0})$,M(x)<0,h′(x)<0,h(x)单调递减,
$x∈({x}_{0},{e}^{t})$,M(x)>0,h′(x)>0,h(x)单调递增,
∵h(x0)<h($\frac{1}{e\sqrt{e}}$)<0,且h(et+t)>(t+1)x2-tx2-t2=x2-t2=(et+t)2-t2>0,
故t>0时,存在唯一的s,使ts2+t2=f(s).
(其中et+t也可取大于et+t,或max{t,et+t}等值).
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z=-3+i | B. | $\overline z=3-i$ | C. | z=1-3i | D. | $\overline z=-1+3i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,1) | D. | D、(-∞,$-\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
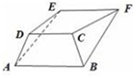 我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )
我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )| A. | 约84立方尺 | B. | 约为105立方尺 | C. | 恰为84立方尺 | D. | 恰为105立方尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点A(2,0),直线l垂直y轴,垂足为点B,线段AB的垂直平分线与l相交于点C,
如图,点A(2,0),直线l垂直y轴,垂足为点B,线段AB的垂直平分线与l相交于点C,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.5 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有97.5%以上的把握认为“市民收入增减与旅游愿望无关” | |
| B. | 有97.5%以上的把握认为“市民收入增减与旅游愿望有关” | |
| C. | 在犯错误的概率不超过0.25%的前提下,认为“市民收入增减与旅游愿望无关” | |
| D. | 在犯错误的概率不超过0.25%的前提下,认为“市民收入增减与旅游愿望有关” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com