
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ①② |
分析 三个平面两两相交、有三条交线,且三条交线不重合,证明时可从三条交线是否存在两条相交入手,假若有两条相交,可以证明两条直线的交点一定经过第三条直线,假若任何两条直线都不相交,根据平面内两条直线平行的定义可得三条交线相互平行
解答 解:如图,
对于①,若a、b、c中任何两条直线都不相交,
∵a?α,b?α,根据同一平面内两条直线不相交则平行,
∴a∥b,同理b∥c.∴a∥b∥c.
综上,平面α∩平面β=a,平面α∩平面γ=b,平面γ∩平面β=c且a、b、c不重合,
则a、b、c交于一点或两两平行.
对于②,若a、b、c中存在两条直线相交,不妨设a∩b=P,
则P∈a,P∈b,∵α∩β=a,∴a?α,则P∈α,α∩γ=b,∴b?γ,则P∈γ,
∴P在α与γ的交线上,即P∈c.∴a、b、c交于一点;
对于③,若a⊥b,b⊥c,则a与c不一定垂直.
故选:D
点评 本题考查了平面的基本性质及其推论,公理3是用来证明点共线及线过同一点的理论依据,本题还考查了分类讨论的数学思想,考查了学生的空间想象和思维能力,此题是中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
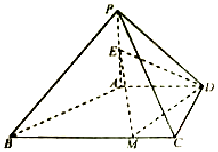 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com