
分析 利用${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{a}_{n}={S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$求解.
解答 解:∵数列{an}的前n项和为${S_n}=\frac{2}{3}{n^2}-\frac{1}{3}n$,
∴n=1时,a1=S1=$\frac{2}{3}-\frac{1}{3}=\frac{1}{3}$,
n≥2时,an=Sn-Sn-1=($\frac{2}{3}{n}^{2}-\frac{1}{3}n$)=[$\frac{2}{3}$(n-1)2-$\frac{1}{3}$(n-1)]=$\frac{4}{3}n-1$,
当n=1时,上式成立,
∴${a}_{n}=\frac{4}{3}n-\frac{1}{3}$.
故答案为:$\frac{4}{3}n-1$.
点评 本题考查数列的通项公式的求法,考查推理论证能力、运算求解能力,考查化归转化思想,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
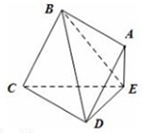 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}({2^n}-1)$ | B. | $\frac{1}{5}(1-{2^{4n}})$ | C. | $\frac{1}{3}({4^n}-1)$ | D. | $\frac{1}{3}(1-{2^n})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
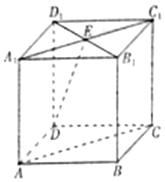 如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.
如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com