
| A. | $\frac{1}{3}({2^n}-1)$ | B. | $\frac{1}{5}(1-{2^{4n}})$ | C. | $\frac{1}{3}({4^n}-1)$ | D. | $\frac{1}{3}(1-{2^n})$ |
分析 由题意可得数列{an}为首项为1,公比为2的等比数列,Sn为首项为1,公比为-4的等比数列前2n项和,运用求和公式即可得到.
解答 解:在数列{an}中,a1=1,an+1=2an,
可得an=2n-1,
${S_n}=a_1^2-a_2^2+a_3^2-a_4^2+$…$+a_{2n-1}^2-a_{2n}^2$
=1-4+16-64+…+42n-2-42n-1
=$\frac{1-(-4)^{2n}}{1-(-4)}$=$\frac{1}{5}$(1-42n)=$\frac{1}{5}$(1-24n).
故选:B.
点评 本题考查等比数列的通项公式和求和公式的运用,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
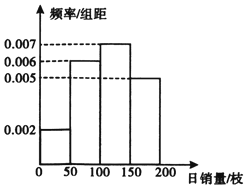 某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.
某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com