
分析 先根据向量的数量积和向量的模,求出|$\overrightarrow{a}$+$\overrightarrow{b}$|=5,再由$({\overrightarrow a-\overrightarrow c})•({\overrightarrow b-\overrightarrow c})=0$,得到$\overrightarrow{c}$|2=5|$\overrightarrow{c}$|cos($\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{c}$),继而求出范围.
解答 解:∵$|{\overrightarrow a}|=3,|{\overrightarrow b}|=4,\overrightarrow a•\overrightarrow b=0$,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=5,
∵$({\overrightarrow a-\overrightarrow c})•({\overrightarrow b-\overrightarrow c})=0$,
∴|$\overrightarrow{c}$|2=($\overrightarrow{a}+\overrightarrow{b}$)•$\overrightarrow{c}$=|($\overrightarrow{a}+\overrightarrow{b}$|•|$\overrightarrow{c}$|cos($\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{c}$)=5|$\overrightarrow{c}$|cos($\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{c}$),
∴|$\overrightarrow{c}$|=0,或|$\overrightarrow{c}$|=5cos($\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{c}$)≤5,
故$|{\overrightarrow c}|$的取值范围[0,5],
故答案为:[0,5]
点评 本题考查了向量的数量积的运算和向量的模,考查了学生的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}({2^n}-1)$ | B. | $\frac{1}{5}(1-{2^{4n}})$ | C. | $\frac{1}{3}({4^n}-1)$ | D. | $\frac{1}{3}(1-{2^n})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
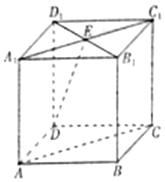 如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.
如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
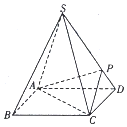 如图,四棱锥S-ABCD的底面边长为1的正方形,每条侧棱的长均为$\sqrt{2}$,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面边长为1的正方形,每条侧棱的长均为$\sqrt{2}$,P为侧棱SD上的点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
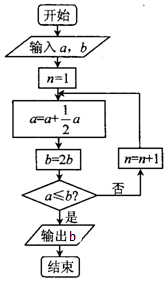 宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )
宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com