
分析 (1)求函数的导数,利用函数的单调性和导数之间的关系,即可求函数f(x)的最小值,f(x)≥0对任意的x∈R恒成立,即在x∈R上,f(x)min≥0;
(2)证明(1-$\frac{k}{n}$)n≤(${e}^{-\frac{k}{n}}$)n=e-k,即可证明($\frac{1}{n}$)n+($\frac{2}{n}$)n+…+($\frac{n-1}{n}$)n+($\frac{n}{n}$)n<$\frac{e}{e-1}$(n∈N*).
解答 解:(1)f(x)≥0对任意的x∈R恒成立,即在x∈R上,f(x)min≥0.
f'(x)=ex-a,
由f'(x)=ex-a=0得x=lna,
由f'(x)>0得,x>lna,此时函数单调递增,
由f'(x)<0得,x<lna,此时函数单调递减,
即f(x)在x=lna处取得极小值且为最小值,
最小值为f(lna)=elna-alna-1=a-alna-1,
设g(a)=a-alna-1,所以g(a)≥0.
由g′(a)=1-lna-1=-lna=0得a=1.
∴g(a)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
∴g(a)在a=1处取得最大值,而g(1)=0.
因此g(a)≥0的解为a=1,∴a=1.
证明:(2)由(1)知,对任意实数x均有ex-x-1≥0,即1+x≤ex.
令$x=-\frac{k}{n}$(n∈N*,k=0,1,2,3,…,n-1),则0<1-$\frac{k}{n}$<e${\;}^{-\frac{k}{n}}$.
∴(1-$\frac{k}{n}$)n≤(${e}^{-\frac{k}{n}}$)n=e-k.
∴($\frac{1}{n}$)n+($\frac{2}{n}$)n+…+($\frac{n-1}{n}$)n+($\frac{n}{n}$)n≤e-(n-1)+e-(n-2)+…+e-2+e-1+1
=$\frac{{1-{e^{-n}}}}{{1-{e^{-1}}}}<\frac{1}{{1-{e^{-1}}}}=\frac{e}{e-1}$.
故($\frac{1}{n}$)n+($\frac{2}{n}$)n+…+($\frac{n-1}{n}$)n+($\frac{n}{n}$)n<$\frac{e}{e-1}$(n∈N*).
点评 本题主要考查函数的单调性和导数的之间关系,以及不等式恒成立问题,考查不等式的证明,将不等式恒成立转化为求函数的最值是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
| 431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
| A. | 0.2 | B. | 0.25 | C. | 0.35 | D. | 0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}({2^n}-1)$ | B. | $\frac{1}{5}(1-{2^{4n}})$ | C. | $\frac{1}{3}({4^n}-1)$ | D. | $\frac{1}{3}(1-{2^n})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
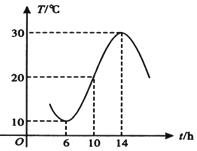 如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b(|ϕ|<π),则这段曲线的函数解析式可以为y=10sin($\frac{π}{8}x+\frac{3π}{4}$)+20;(6≤x≤14).
如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b(|ϕ|<π),则这段曲线的函数解析式可以为y=10sin($\frac{π}{8}x+\frac{3π}{4}$)+20;(6≤x≤14).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com