
分析 (Ⅰ)若a≥2,f(a2)=2(a-$\frac{1}{4}$)2-$\frac{9}{8}$,即可求f(a2)的最小值;
(Ⅱ)若f(x)最小值是2,分类讨论,即可求实数a的值.
解答 解:(Ⅰ)∵a≥2,∴a2>a,
∵f(x)=|x-1|+|x-a|,∴f(a2)=2a2-a-1,即f(a2)=2(a-$\frac{1}{4}$)2-$\frac{9}{8}$.
∴f(a2)min=5.…(5分)
(Ⅱ)当a=1时,f(x)=2|x-1|,f(x)min=0,舍.…(6分)
当a<1时,f(x)=$\left\{\begin{array}{l}{-2x+a+1,}&{x<a}\\{1-a,}&{a≤x≤1}\\{2x-a-1,}&{x>1}\end{array}\right.$,∴f(x)min=1-a,…(7分)
由题意,1-a=2,∴a=-1.…(8分)
当a>1时,f(x)=$\left\{\begin{array}{l}{-2x+a+1,}&{x<1}\\{a-1,}&{1≤x≤a}\\{2x-a-1,}&{x>a}\end{array}\right.$,∴f(x)min=a-1,
∴a-1=2,∴a=3.…(9分)
点评 本题考查记不住不等式,考查分类讨论的数学思想,正确转化是关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}({2^n}-1)$ | B. | $\frac{1}{5}(1-{2^{4n}})$ | C. | $\frac{1}{3}({4^n}-1)$ | D. | $\frac{1}{3}(1-{2^n})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
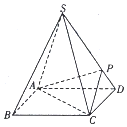 如图,四棱锥S-ABCD的底面边长为1的正方形,每条侧棱的长均为$\sqrt{2}$,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面边长为1的正方形,每条侧棱的长均为$\sqrt{2}$,P为侧棱SD上的点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 32 | C. | 48 | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
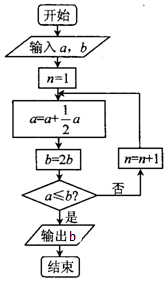 宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )
宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [1,2) | C. | [-2,∞) | D. | (-2,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com