
| A. | 53 | B. | 59 | C. | 66 | D. | 71 |
分析 根据题意,分析可得四位数字相加和为10的情况有①0、1、3、6,②0、1、4、5,③0、1、2、7,④0、2、3、5,⑤1、2、3、4;共5种情况,据此分5种情况讨论,依次求出每种情况下大于2017的“完美四位数”的个数,将其相加即可得答案.
解答 解:根据题意,四位数字相加和为10的情况有①0、1、3、6,②0、1、4、5,③0、1、2、7,④0、2、3、5,⑤1、2、3、4;共5种情况,
则分5种情况讨论:
①、四个数字为0、1、3、6时,
千位数字可以为3或6,有2种情况,将其余3个数字全排列,安排在百位、十位、个位,有A33=6种情况,
此时有2×6=12个“完美四位数”,
②、四个数字为0、1、4、5时,
千位数字可以为4或5,有2种情况,将其余3个数字全排列,安排在百位、十位、个位,有A33=6种情况,
此时有2×6=12个“完美四位数”,
③、四个数字为0、1、2、7时,
千位数字为7时,将其余3个数字全排列,安排在百位、十位、个位,有A33=6种情况,
千位数字为2时,有2071、2107、2170、2701、2710,共5种情况,
此时有6+5=11个“完美四位数”,
④、四个数字为0、2、3、5时,
千位数字可以为2或3或5,有3种情况,将其余3个数字全排列,安排在百位、十位、个位,有A33=6种情况,
此时有3×6=18个“完美四位数”,
⑤、四个数字为1、2、3、4时,
千位数字可以为3或4或2,有3种情况,将其余3个数字全排列,安排在百位、十位、个位,有A33=6种情况,
此时有3×6=18个“完美四位数”,
则一共有12+12+11+18+18=71个“完美四位数”,
故选:D.
点评 本题考查排列、组合的应用,涉及分类计数原理的运用,分类讨论注意做到不重不漏.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有一个对称中心$({\frac{π}{12},0})$ | B. | 有一条对称轴$x=\frac{π}{6}$ | ||
| C. | 在区间$[{-\frac{π}{12},\frac{5π}{12}}]$上单调递减 | D. | 在区间$[{-\frac{5π}{12},\frac{π}{12}}]$上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
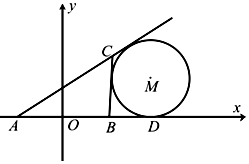 如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com