
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
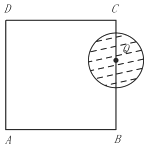 如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )
如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )| A. | $[{1-\frac{{\sqrt{2}}}{4},2+\frac{{\sqrt{2}}}{4}}]$ | B. | $[{\frac{3}{4},2+\frac{{\sqrt{2}}}{4}}]$ | C. | $[{\frac{3}{4},\frac{9}{4}}]$ | D. | $[{1-\frac{{\sqrt{2}}}{4},\frac{9}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{2}$ | B. | 2 | C. | 2+$\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<m<1 | B. | -4<m<0 | C. | m<1 | D. | -3<m<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的A点处,乙船在中间B点处,丙船在最后面的C点处,且BC:AB=3:1.一架无人机在空中的P点处对它们进行数据测量,在同一时刻测得∠APB=30°,∠BPC=90°.(船只与无人机的大小及其它因素忽略不计)
如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的A点处,乙船在中间B点处,丙船在最后面的C点处,且BC:AB=3:1.一架无人机在空中的P点处对它们进行数据测量,在同一时刻测得∠APB=30°,∠BPC=90°.(船只与无人机的大小及其它因素忽略不计)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com