
| A. | (4,-7) | B. | (-2,11) | C. | (4,-7)和(-2,11) | D. | (-2,11)和(1,2) |
分析 设P(m,n),根据题意得$\overrightarrow{{P}_{1}P}$=-2$\overrightarrow{P{P}_{2}}$,由此建立关于m、n的方程组,解之即可得到点P的坐标.
解答 解:∵P在线段P1P2的延长线上,且|$\overrightarrow{{P}_{1}P}$|=2|$\overrightarrow{P{P}_{2}}$|,
∴$\overrightarrow{{P}_{1}P}$=-2$\overrightarrow{P{P}_{2}}$,
∵P1(2,-1),P2(0,5),
∴设P(m,n),可得$\overrightarrow{{P}_{1}P}$=(m-2,n+1),$\overrightarrow{P{P}_{2}}$=(-m,5-n)
由此可得$\left\{\begin{array}{l}{m-2=2m}\\{n+1=2n-10}\end{array}\right.$,解之得m=-2,n=11
所以点P的坐标为(-2,11).
故选:B.
点评 本题给出线段P1P2的延长线上满足定比的分点,求该点的坐标.着重考查了向量的坐标运算和两点间距离公式等知识,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 若直线a,b与平面α所成角都是30°,则这两条直线平行 | |
| B. | 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直 | |
| C. | 若直线a,b平行,则这两条直线中至少有一条与平面α平行 | |
| D. | 若直线a,b垂直,则这两条直线与平面α不可能都垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
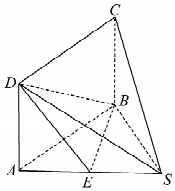 如图,在四棱锥S-ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,$SC=\sqrt{13}$.
如图,在四棱锥S-ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,$SC=\sqrt{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,14] | B. | [-14,1] | C. | [-2,13] | D. | [-13,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com