练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知平面α及直线a，b，则下列说法正确的是（　　）
    A．若直线a，b与平面α所成角都是30°，则这两条直线平行
    B．若直线a，b与平面α所成角都是30°，则这两条直线不可能垂直
    C．若直线a，b平行，则这两条直线中至少有一条与平面α平行
    D．若直线a，b垂直，则这两条直线与平面α不可能都垂直

    分析 两条平行线可以和一个平面成相等的角；两条相交线可以和一个平面成相等的角；两条异面直线可以和一个平面成相等的角，可以判定A，B；
    对C，显然错；
    D，根据若两条直线与平面α都垂直，则线a，b平行，可以判断；

    解答 解：对于A，若直线a，b与平面α所成角都是30°，则这两条直线平行、相交、异面，故错；
    对于B，若直线a，b与平面α所成角都是30°，则这两条直线可能垂直，
    如下图，直角三角形ACB的直角动点在平面α内，边AC、BC可以与平面都成300角，故错．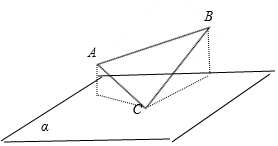

    对于C，若直线a，b平行，则这两条直线中至少有一条与平面α平行，显然错；
    对于D，若两条直线与平面α都垂直，则线a，b平行，故正确；
    故选：D，

    点评 本题考查两直线的位置关系的判断，直线与平面所成角位置关系的判断，是中档题，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=x3-3x2-9x+2，求函数f（x）在区间[-2，2]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．某程序框图如图所示，若输出的p值为31，则判断框内应填入的不等式是（　　）
    A．n＞2B．n＞3C．n＞4D．n＞5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知函数f（x）=$\frac{（x-2）（x+a）}{{x}^{2}}$为偶函数，则a=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=|x+2|-m，m∈R，且f（x）≤0的解集为[-3，-1]
    （1）求m的值；
    （2）设 a、b、c 为正数，且 a+b+c=m，求.$\sqrt{3a+1}$+$\sqrt{3b+1}$+$\sqrt{3c+1}$的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分別为A，B，点M，N是椭圆C上关于长轴对称的两点，若直线AM与BN相交于点P，则点P的轨迹方程是（　　）
    A．x=±a（y≠0）B．y2=2b（|x|-a）（y≠0）
    C．x2+y2=a2+b2（y≠0）D．$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（y≠0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

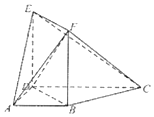    10．如图，梯形ABCD中，∠BAD=∠ADC=90°，CD=2，AD=AB=1，四边形BDEF为正方形，且平面BDEF丄平面ABCD
    （1）求证：DF⊥CE
    （2）若AC与BD相交于点O，那么在棱AE上是否存在点G，使得平面OBG∥平面EFC？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．在△ABC中，∠ABC=120°，BA=2，BC=3，D，E是线段AC的三等分点，则$\overrightarrow{BD}$•$\overrightarrow{BE}$的值为（　　）
    A．$\frac{65}{9}$B．$\frac{11}{9}$C．$\frac{41}{9}$D．-$\frac{13}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知P1（2，-1），P2（0，5），点P在线段P1P2的延长线上，且|$\overrightarrow{{P}_{1}P}$|=2|$\overrightarrow{P{P}_{2}}$|，则点P的坐标（　　）
    A．（4，-7）B．（-2，11）C．（4，-7）和（-2，11）D．（-2，11）和（1，2）

    查看答案和解析>>

    同步练习册答案