Question

3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分別为A，B，点M，N是椭圆C上关于长轴对称的两点，若直线AM与BN相交于点P，则点P的轨迹方程是（　　）

• A． x=±a（y≠0）
• B． y²=2b（|x|-a）（y≠0）
• C． x²+y²=a²+b²（y≠0）
• D． $\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（y≠0）

Answer 1

分析 求得直线PA的方程及PB的方程，两式相乘，整理即可求得P的轨迹方程．

解答 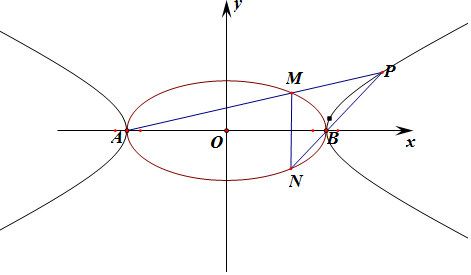解：由题意可知：A（-a，0），B（a，0），设M（x₀，y₀），N（x₀，-y₀），y₀≠0，P（x，y），y≠0
则直线PA的斜率k=$\frac{{y}_{0}}{{x}_{0}+a}$，则直线PA的方程y=$\frac{{y}_{0}}{{x}_{0}+a}$（x+a），①
同理直线PB的斜率k=$\frac{{y}_{0}}{a-{x}_{0}}$，直线PB的方程y=$\frac{{y}_{0}}{a-{x}_{0}}$（x-a），②
两式相乘：y²=$\frac{{y}_{0}^{2}}{{a}^{2}-{x}_{0}^{2}}$（x²-a²），
由$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$，y₀²=$\frac{{b}^{2}}{{a}^{2}}$（a²-x₀²），
则y²=$\frac{{b}^{2}}{{a}^{2}}$（x²-a²），整理得：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）（y≠0），
则点P的轨迹方程$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）（y≠0），
故选D．

点评 本题考查椭圆的标准方程，直线的点斜式方程，考查轨迹方程的求法，考查转化思想，属于中档题．