
| A. | (9,21) | B. | (20,32) | C. | (8,24) | D. | (15,25) |
分析 画出函数f(x)的图象,确定x1x2=1,x3+x4=12,2<x3<x4<10,由此可得$\frac{({x}_{3}-1)•({x}_{4}-1)}{{x}_{1}•{x}_{2}}$的取值范围.
解答 解:函数的图象如图所示,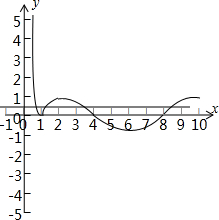
∵f(x1)=f(x2),
∴-log2x1=log2x2,
∴log2x1x2=0,
∴x1x2=1,
∵f(x3)=f(x4),
∴x3+x4=12,2<x3<x4<10
∴$\frac{({x}_{3}-1)•({x}_{4}-1)}{{x}_{1}•{x}_{2}}$=x3x4-(x3+x4)+1=x3x4-11,
∵2<x3<x4<10
∴$\frac{({x}_{3}-1)•({x}_{4}-1)}{{x}_{1}•{x}_{2}}$的取值范围是(9,21).
故选:A
点评 本小题主要考查分段函数的解析式求法及其图象的作法、函数的值域的应用、函数与方程的综合运用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
| 喜欢外卖 | 不喜欢外卖 | 合计 | |
| 90后 | 20 | 5 | 25 |
| 80后 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=±a(y≠0) | B. | y2=2b(|x|-a)(y≠0) | ||
| C. | x2+y2=a2+b2(y≠0) | D. | $\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(y≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
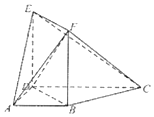 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{65}{9}$ | B. | $\frac{11}{9}$ | C. | $\frac{41}{9}$ | D. | -$\frac{13}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [-2,1] | C. | [0,1] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com