
分析 先求出$\frac{1}{2}$≤log2x≤2,再根据二次函数即可得到结论.
解答 解:由2x≤16得x≤4,log2x≤2,
即$\frac{1}{2}$≤log2x≤2,
$f(x)={log_2}\frac{x}{2}•{log_{\sqrt{2}}}\frac{{\sqrt{x}}}{2}$=(log2x-1)(log2x-2)=(log2x-$\frac{3}{2}$)2-$\frac{1}{4}$,
当${log_2}x=\frac{3}{2}$,$f{(x)_{min}}=-\frac{1}{4}$,当${log_2}x=\frac{1}{2}$,$f{(x)_{max}}=\frac{3}{4}$,
故f(x)的取值范围为$[-\frac{1}{4},\frac{3}{4}]$.
点评 本题主要考查函数值域的计算,根据二次函数是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
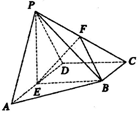 在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.
在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,4} | B. | {1,5} | C. | {2,4} | D. | {2,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com