
分析 (1)设N(x,y),M(x′,y′),由于$\overrightarrow{ON}=2\overrightarrow{OM}$,由$\left\{\begin{array}{l}{x=2{x}^{′}}\\{y=2{y}^{′}}\end{array}\right.$,可得$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{2}x}\\{{y}^{′}=\frac{1}{2}y}\end{array}\right.$代入曲线C1的参数方程$\left\{\begin{array}{l}{{x}^{′}=cosα}\\{{y}^{′}=2sinα}\end{array}\right.$为参数),化简整理即可得出;
(2)由曲线C3的极坐标方程是ρ=2,化为x2+y2=4,由题意可得:A,B,C三点的直角坐标分别为$A(\sqrt{3},1),B(-\sqrt{3},1),C(0,-2)$,设P(2cosα,4sinα),利用两点之间的距离即可得出.
解答 解:(1)设N(x,y),M(x′,y′),由于$\overrightarrow{ON}=2\overrightarrow{OM}$,
∴$\left\{\begin{array}{l}{x=2{x}^{′}}\\{y=2{y}^{′}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{2}x}\\{{y}^{′}=\frac{1}{2}y}\end{array}\right.$代入曲线C1的参数方程$\left\{\begin{array}{l}{{x}^{′}=cosα}\\{{y}^{′}=2sinα}\end{array}\right.$为参数),可得$\left\{\begin{array}{l}{\frac{1}{2}x=cosα}\\{\frac{1}{2}y=2sinα}\end{array}\right.$,
化为$\frac{{y}^{2}}{16}+$$\frac{{x}^{2}}{4}$=1.
(2)由曲线C3的极坐标方程是ρ=2,化为x2+y2=4,
A,B,C三点的直角坐标分别为$A(\sqrt{3},1),B(-\sqrt{3},1),C(0,-2)$,
设P(2cosα,4sinα),
∴|PA|2+|PB|2+|PC|2=36sin2α+24.
∵sin2α∈[0,1],
∴|PA|2+|PB|2+|PC|2的取值范围是[24,60].
点评 本题考查了椭圆的参数方程及其变换、圆的极坐标方程、三角函数的单调性与值域两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{12}^{10}$($\frac{3}{8}$)10($\frac{5}{8}$)2 | B. | C${\;}_{12}^{9}$($\frac{3}{8}$)9($\frac{5}{8}$)2($\frac{3}{8}$) | C. | C${\;}_{11}^{9}$($\frac{5}{8}$)9($\frac{3}{8}$)2 | D. | C${\;}_{11}^{9}$($\frac{3}{8}$)10($\frac{5}{8}$)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-3=0 | B. | 2x+y-3=0 | C. | x+y-1=0 | D. | x+y-3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
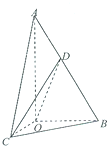 如图,在Rt△AOB中,∠OAB=30°,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C的直二面角,D是AB的中点.
如图,在Rt△AOB中,∠OAB=30°,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C的直二面角,D是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com