
【题目】已知关于x的不等式(m﹣1)x2+(m﹣1)x+2>0
(1)若m=0,求该不等式的解集
(2)若该不等式的解集是R,求m的取值范围.
【答案】
(1)解:不等式(m﹣1)x2+(m﹣1)x+2>0,当m=0时,可得不等式x2+x﹣2<0,等价于与(x+2)(x﹣1)<0,
解得:﹣2<x<1,
∴不等式的解集为(﹣2,1).
(2)解:不等式(m﹣1)x2+(m﹣1)x+2>0,
当m=1时,可得不等式为2,显然成立,
不等式大于0,解集是R,
则m>1,△<0,即(m﹣1)2﹣8(m+1)<0,
解得:1<m<9,
综上可得:
m的取值范围是:{m|1≤m<9}.
【解析】(1)当m=0时,化简不等式,即可求解.(2)对m讨论,然后根据不等式大于0,解集是R,开口向上,判别式小于0,即可得m的取值范围.
【考点精析】解答此题的关键在于理解解一元二次不等式的相关知识,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知a+b=5,c= ![]() ,且4sin2
,且4sin2 ![]() ﹣cos2C=
﹣cos2C= ![]()
(1)求角C的大小;
(2)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PC⊥平面ABC,∠PAC=30°,∠ACB=45°,BC=2 ![]() ,PA⊥AB.
,PA⊥AB. 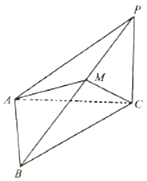
(1)求PC的长;
(2)若点M在侧棱PB上,且 ![]() ,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估.该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入 ![]() 万作为技改费用,投入(50+2x)万元作为宣传费用.试问:当该商品改革后的销售量a至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
万作为技改费用,投入(50+2x)万元作为宣传费用.试问:当该商品改革后的销售量a至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形, ![]() ,AB⊥AD,AB∥CD,点M是PC的中点. (I)求证:MB∥平面PAD;
,AB⊥AD,AB∥CD,点M是PC的中点. (I)求证:MB∥平面PAD;
(II)求二面角P﹣BC﹣D的余弦值.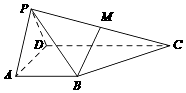
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心. 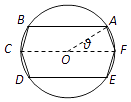
(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);
(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com