
����Ŀ��ijӪ��ѧ�ҽ��飺������ÿ��ĵ�����������������[60��90]����λ���ˣ���֬����������������[18��27]����λ���ˣ���ijѧУʳ���ṩ�Ļ�ʳ��ʳ��A��ʳ��BΪ����1ǧ��ʳ��A��������60�ˣ���֬��9�ˣ��ۼ�20Ԫ��1ǧ��ʳ��B��������30�ˣ���֬��27�ˣ��ۼ�15Ԫ�� �������ijѧ��ֻ��ʳ��A���ж����Ļ�ʳ�Ƿ����Ӫ��ѧ�ҵĽ��飬��˵�����ɣ�
����Ϊ�˻�������ҷ���Ӫ��ѧ�ҵĽ��飬ѧ����Ҫÿ��ͬʱʳ��ʳ��A��ʳ��B������ǧ�ˣ�����������Ҫ���ѵ�Ǯ����
���𰸡��⣺�������ѧ��ֻ��ʳ��Axkg�� �� ![]() ��
��
�⣬
�ʲ�����Ӫ��ѧ�ҵĽ��飻
���������⣬��ѧ��ÿ���ʳ��Axkg��ʳ��Bykg��
��z=20x+15y��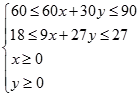
��ƽ���������£�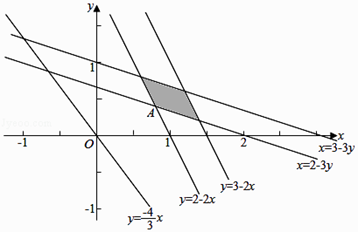 ��
��
�� ![]() ��ã�x=
��ã�x= ![]() ��y=
��y= ![]() ��
��
��z=20�� ![]() +15��
+15�� ![]() =22��
=22��
��ѧ��ÿ���0.8ǧ��ʳ��A��0.4ǧ��ʳ��B�����ܷ���Ӫ��ѧ�ҵĽ����ֻ������٣�
�����Ҫ����22Ԫ
���������������ѧ��ֻ��ʳ��Axkg���Ӷ��ò���ʽ�� ![]() ���Ƿ��н⼴�ɣ����������⣬��ѧ��ÿ���ʳ��Axkg��ʳ��Bykg���Ӷ��õ�Ŀ�꺯��z=20x+15y������Լ������
���Ƿ��н⼴�ɣ����������⣬��ѧ��ÿ���ʳ��Axkg��ʳ��Bykg���Ӷ��õ�Ŀ�꺯��z=20x+15y������Լ������ 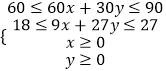 ���Ӷ��������Թ滮��⼴�ɣ�
���Ӷ��������Թ滮��⼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����б������ABC��A1B1C1��BC��CC1 �� AC=BC=2��A1�ڵ���ABC�ϵ���ӰǡΪAC���е�D�� 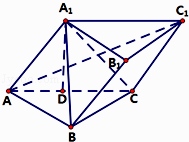
��1��֤����BC��ƽ��ACC1A1
��2���������A��A1B��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() =��1��2����
=��1��2���� ![]() =����3��4����
=����3��4����
��1���� ![]() +
+ ![]() ��
�� ![]() ��
�� ![]() �ļнǣ�
�ļнǣ�
��2���� ![]() ����
���� ![]() �ͣ�
�ͣ� ![]() +
+ ![]() ������
������ ![]() +
+ ![]() ����
���� ![]() ����
���� ![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=loga��x+2����1��a��0��a��1����ͼ��������A������A��ֱ��mx+ny+1=0�ϣ�����m��0��n��0���� ![]() +
+ ![]() ����СֵΪ�� ��
����СֵΪ�� ��
A.3+2 ![]()
B.3+2 ![]()
C.7
D.11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪R��x0 �� y0������Բ ![]() +
+ ![]() =1�ϵ�һ�㣬��ԭ��O��ԲR��x��x0��2+��y��y0��2=12���������ߣ��ֱ���Բ��P��Q���㣮
=1�ϵ�һ�㣬��ԭ��O��ԲR��x��x0��2+��y��y0��2=12���������ߣ��ֱ���Բ��P��Q���㣮 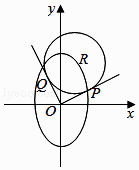
��1����R���ڵ�һ���ޣ���ֱ��OP��OQ���ഹֱ����ԲR�ķ��̣�
��2����ֱ��OP��OQ��б�ʴ��ڣ��ֱ��Ϊk1 �� k2 �� ��k1k2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABCD�У�����ABCD�����Σ�PA�͵���ABCD��M����PC��һ�㣮��PA=AC=a����MBD�����Ϊ��Сֵʱ��ֱ��AC��ƽ��MBD���ɵĽ�Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������� ABCD �У�AB ��Ϊ 2 ǧ�ף�BC ��Ϊ 1 ǧ�ף��� A ��� C �㴦����һ��ͨ�Ż�վ���串�Ƿ�Χ��Ϊ��Բ 1 ǧ�ף����ڸþ�������������ѡȡһ�ص㣬��õص����źŵĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ����M��P=R�������н�����һ����ȷ���ǣ� ��
����M��P=R�������н�����һ����ȷ���ǣ� ��
A.����f��x��һ���������ֵ
B.����f��x��һ��������Сֵ
C.����f��x��һ�����������ֵ
D.����f��x��һ����������Сֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ȳ�����{an}����a3=5��a10=��9�� ������{an}��ͨ�ʽ��
������{an}��ǰn���Sn��ʹ��Sn�������n��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com