练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知数列{xn}为等差数列，且x1+x2+x3=5，x18+x19+x20=25，则数列{xn}的前20项的和为100．

    分析 通过等差中项可知x2=$\frac{5}{3}$，x19=$\frac{25}{3}$，利用数列{xn}的前20项的和为$\frac{20（{x}_{2}+{x}_{19}）}{2}$，进而计算可得结论．

    解答 解：∵数列{xn}为等差数列，
    ∴2xn+1=xn+xn+2，
    又∵x1+x2+x3=5，x18+x19+x20=25，
    ∴x2=$\frac{5}{3}$，x19=$\frac{25}{3}$，
    ∴x2+x19=$\frac{5}{3}$+$\frac{25}{3}$=10，
    ∴数列{xn}的前20项的和为$\frac{20（{x}_{2}+{x}_{19}）}{2}$=100，
    故答案为：100．

    点评 本题考查数列的前n项和，考查运算求解能力，注意解题方法的积累，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知f（x）是定义在R上的偶函数，当x≥0时，f（x）=x2-4x+1，则不等式f（x）＞2x2-4的解集为（　　）
    A．（-1，2）B．（-1，1）C．[0，1]D．（-1，0]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．使不等式|x+1|≤4成立的一个必要不充分条件是（　　）
    A．2≤x≤3B．-6≤x≤3C．-5≤x≤3D．-6≤x≤2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知命题p：关于x的方程4x2-2ax+2a+5=0最多只有一个实根，命题q：{x|x2-2x+1-m2≤0，m＞0}．若非p是非q的必要不充分条件，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．若tanα=3，则sin2α+2cos2α=$\frac{11}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设集合A={x|-2＜x＜7 }，B={x|x＞1，x∈N}，则A∩B的元素的个数为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

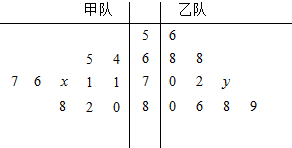    19．下面的茎叶图记录了甲、乙两代表队各10名同学在一次数学竞赛中的成绩（单位：分），已知甲代表队数据的中位数为76，乙代表队数据的平均数是75．
    （1）求x，y的值，并判断甲、乙两队谁的成绩更稳定？（不需要说明理由）
    （2）若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生，求抽到学生中，甲队学生成绩不低于乙队学生成绩的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知圆x2+y2=4，过点A（4，0）作圆的割线ABC，则弦BC中点的轨迹方程为（　　）
    A．（x-1）2+y2=4  （-1≤x＜$\frac{1}{2}$）B．（x-1）2+y2=4　（0≤x＜1）
    C．（x-2）2+y2=4  （-1≤x＜$\frac{1}{2}$）D．（x-2）2+y2=4　（0≤x＜1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．有四个命题
    ①p：f（x）=lnx-2+λ在区间（1，2）上有一个零点，q：e0.2＞e0.3，p∧q为真命题
    ②当x＞1时，f（x）=x2，g（x）=x${\;}^{\frac{1}{3}}$，h（x）=x-2的大小关系是h（x）＜g（x）＜f（x）
    ③若f′（x0）=0，则f（x）在x=x0处取得极值
    ④若不等式2-3x-2x2＞0的解集为P，函数y=$\sqrt{x+2}$+$\sqrt{1-2x}$的定义域为Q，则“x∈P”是“x∈Q”的充分不必要条件，其中正确命题的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    同步练习册答案