
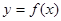 是定义在
是定义在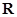 上的奇函数,且当
上的奇函数,且当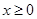 时,
时,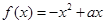 .
.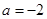 时,求函数
时,求函数 的解析式;
的解析式; 为单调递减函数;
为单调递减函数; 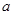 的范围(不必证明);
的范围(不必证明);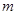 ,
,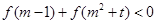 恒成立,求实数
恒成立,求实数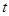 的取值范围.
的取值范围.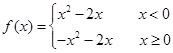 ;(2)
;(2)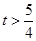 。
。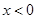 时,
时,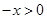 ,又因为
,又因为 为奇函数,所以
为奇函数,所以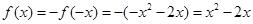 ,进而得到解析式。
,进而得到解析式。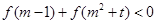 ,∴
,∴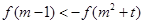
 是奇函数,∴
是奇函数,∴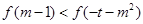 ,而又因为
,而又因为 为
为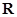 上的单调递减函数,所以
上的单调递减函数,所以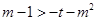 恒成立,分离参数的思想得到范围。
恒成立,分离参数的思想得到范围。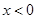 时,
时,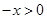 ,又因为
,又因为 为奇函数,
为奇函数,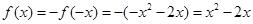
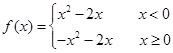 …………………………6分
…………………………6分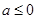 时,对称轴
时,对称轴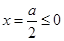 ,所以
,所以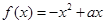 在
在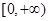 上单调递减,
上单调递减, 在
在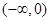 上单调递减,
上单调递减,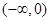 上
上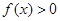 ,在
,在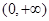 上
上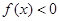 ,
,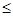 0时,
0时,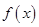 为R上的单调递减函数
为R上的单调递减函数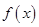 在
在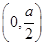 上递增,在
上递增,在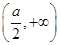 上递减,不合题意
上递减,不合题意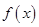 为单调函数时,a的范围为a
为单调函数时,a的范围为a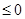 ………………………………………….10分
………………………………………….10分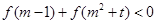 ,∴
,∴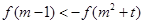
 是奇函数,∴
是奇函数,∴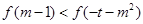 …………………………12分
…………………………12分 为
为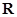 上的单调递减函数,所以
上的单调递减函数,所以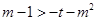 恒成立,…………………14分
恒成立,…………………14分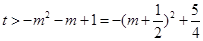 恒成立, 所以
恒成立, 所以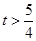 …………………………16分
…………………………16分

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com