
分析 (Ⅰ)设函数f(x)=ax2+bx+c,由f(0)=0⇒c=0,利用f(x)≤6x+2,可得对任意的x∈R恒成立,必有b<4且△≤0,整理得b=2,即可确定函数y=f(x)的解析式;
(Ⅱ)由an+1=f(an)=-2an2+2an,所以an+1-an=-2(an-$\frac{1}{4}$)2+$\frac{1}{8}$.要证an+1>an,即证-2(an-$\frac{1}{4}$)2+$\frac{1}{8}$>0,只要证an∈(0,$\frac{1}{2}$),利用数学归纳法进行证明即可;
(Ⅲ)由(Ⅱ)可得,an∈(0,$\frac{1}{2}$),可得不等式的右边;再由an=$\frac{1}{2}$-$\frac{1}{2•{3}^{{2}^{n-1}}}$,运用不等式的性质和等比数列的求和公式即可得到不等式的左边成立.
解答 解:(I)设函数f(x)=ax2+bx+c,
由f(0)=0,可得c=0,
令-3x2-1=6x+2,有x2+2x+1=0,即x=-1,
故f(-1)=-4,所以a-b=-4,
所以f(x)=(b-4)x2+bx,
由f(x)≤6x+2得(b-4)x2+(b-6)x-2≤0,
对任意的x∈R恒成立,必有b<4且△≤0,
整理得(b-2)2≤0,解得b=2,a=-2,
所以f(x)=-2x2+2x;
(Ⅱ)证明:因为an+1=f(an)=-2an2+2an,
所以an+1-an=-2(an-$\frac{1}{4}$)2+$\frac{1}{8}$.
要证an+1>an,即证-2(an-$\frac{1}{4}$)2+$\frac{1}{8}$>0,
只要证an∈(0,$\frac{1}{2}$),
当n=1,a1=$\frac{1}{3}$∈(0,$\frac{1}{2}$),显然成立;
设n=k时,ak∈(0,$\frac{1}{2}$),
则ak+1=-2ak2+2ak=-2(ak-$\frac{1}{2}$)2+$\frac{1}{2}$∈(0,$\frac{1}{2}$),
综上对?n∈N*,an∈(0,$\frac{1}{2}$),
所以an+1>an;
(Ⅲ)证明:由(Ⅱ)可得,an∈(0,$\frac{1}{2}$),
可得a1+a2+…+an<$\frac{n}{2}$成立;
由a1=$\frac{1}{3}$=$\frac{1}{2}$-$\frac{1}{2•3}$,a2=$\frac{4}{9}$=$\frac{1}{2}$-$\frac{1}{2•{3}^{2}}$,
a3=$\frac{40}{81}$=$\frac{1}{2}$-$\frac{1}{2•{3}^{4}}$,…,an=$\frac{1}{2}$-$\frac{1}{2•{3}^{{2}^{n-1}}}$,
即有a1+a2+…+an=$\frac{n}{2}$-$\frac{1}{2}$($\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{4}}$+…+$\frac{1}{{3}^{{2}^{n-1}}}$)
>$\frac{n}{2}$-$\frac{1}{2}$($\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$)
=$\frac{n}{2}$-$\frac{1}{2}$•$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$=$\frac{n}{2}$-$\frac{1}{4}$(1-$\frac{1}{{3}^{n}}$)>$\frac{n}{2}$-$\frac{1}{4}$.
综上可得,$\frac{n}{2}$-$\frac{1}{4}$≤a1+a2+…+an<$\frac{n}{2}$(n∈N+).
点评 本题考查二次函数的解析式的求法,注意运用待定系数法和判别式法,考查不等式的证明,注意运用数学归纳法和不等式的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {1,3,4} | C. | {1,4,5} | D. | {2,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
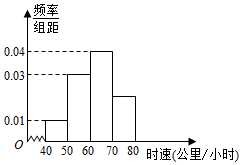 已知某一段公路限速70公里/小时,现抽取400辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这400辆汽车中在该路段超速的有80辆.
已知某一段公路限速70公里/小时,现抽取400辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这400辆汽车中在该路段超速的有80辆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个平面内有无数条直线平行于另一个平面 | |
| B. | 一个平面内有两条直线平行于另一个平面 | |
| C. | 一个平面内有两条相交直线平行于另一个平面 | |
| D. | 两个平面同时垂直于另一个平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
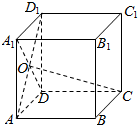
| A. | 线段DO | B. | 线段D1O | C. | 线段A1O | D. | 线段AO |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∠BAC=∠B′A′C′ | |
| B. | ∠BAC+∠B′A′C′=180° | |
| C. | ∠BAC=∠B′A′C′或∠BAC+∠B′A′C′=180° | |
| D. | ∠BAC>∠B′A′C′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com