
分析 设直线方程为:y=k(x+2)+1,代入抛物线方程得k2x2+(4k2+2k-4)x+4k2+4k+1=0(*),直线与抛物线只有一个公共点等价于(*)只有一个根,由此能求出结果.
解答 解:由题意可设直线方程为:y=k(x+2)+1,
代入抛物线方程整理可得k2x2+(4k2+2k-4)x+4k2+4k+1=0(*),
直线与抛物线只有一个公共点等价于(*)只有一个根,
①k=0时,y=1符合题意;
②k≠0时,△=(4k2+2k-4)2-4k2(4k2+4k+1)=0,整理,得2k2+k-1=0,
解得k=$\frac{1}{2}$或k=-1.
综上可得,k=$\frac{1}{2}$或k=-1或k=0时,直线l与抛物线只有一个公共点,
对应的直线l的方程分别为:y=$\frac{1}{2}(x+2)+1$,y=-(x+2)+1,y=1,
即x-2y+4=0,x+y+1=0,y=1.
点评 本题考查满足条件的直线的斜有一些及直线方程的求法,是中档题,解题时要认真审题,注意直线与抛物线的位置关系的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
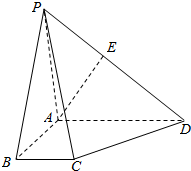 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E是PD的中点.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{{{x^2}-1}}{x-1}与y=x+1$ | B. | $y=lgx与y=\frac{1}{2}lg{x^2}$ | ||
| C. | y=lg(x2-1)与y=lg(x+1)+lg(x-1) | D. | y=x与y=${log}_{a}{a}^{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知点D、E、F分别为△ABC的边BC、CA、AB上的点,AD、BE、CF相交于点P,且AE=EC,BF=2FA.
已知点D、E、F分别为△ABC的边BC、CA、AB上的点,AD、BE、CF相交于点P,且AE=EC,BF=2FA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com