
 已知点D、E、F分别为△ABC的边BC、CA、AB上的点,AD、BE、CF相交于点P,且AE=EC,BF=2FA.
已知点D、E、F分别为△ABC的边BC、CA、AB上的点,AD、BE、CF相交于点P,且AE=EC,BF=2FA.分析 (1)由B,P,E三点共线便可得到$\overrightarrow{BP}=λ\overrightarrow{BE}$,从而可得到$\overrightarrow{AP}=(1-λ)\overrightarrow{AB}+\frac{λ}{2}\overrightarrow{AC}$,这样同理可以由C,P,F三点共线得到$\overrightarrow{AP}=(1-μ)\overrightarrow{AC}+\frac{μ}{3}\overrightarrow{AB}$,从而由平面向量基本定理即可建立关于λ,μ的二元一次方程组,解出$\left\{\begin{array}{l}{λ=\frac{4}{5}}\\{μ=\frac{3}{5}}\end{array}\right.$,这样即可表示出$\overrightarrow{BP}=-\frac{4}{5}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b}$,$\overrightarrow{CP}=\frac{1}{5}\overrightarrow{a}-\frac{3}{5}\overrightarrow{b}$;
(2)可设$\overrightarrow{BD}=x(\overrightarrow{b}-\overrightarrow{a})$,从而可得到$\overrightarrow{AD}=(1-x)\overrightarrow{a}+x\overrightarrow{b}$,而求出$\overrightarrow{AP}=\frac{1}{5}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b}$,$\overrightarrow{AD}$与$\overrightarrow{AP}$共线,从而有$\overrightarrow{AD}=k\overrightarrow{AP}$,这样即可建立关于x,k的二元一次方程组,解出x便可得出BD:DC的值.
解答 解:(1)B,P,E三点共线;
∴存在λ,使$\overrightarrow{BP}=λ\overrightarrow{BE}$;
∴$\overrightarrow{AP}-\overrightarrow{AB}=λ(\overrightarrow{AE}-\overrightarrow{AB})$;
∴$\overrightarrow{AP}-\overrightarrow{AB}=λ(\frac{1}{2}\overrightarrow{AC}-\overrightarrow{AB})$;
∴$\overrightarrow{AP}=(1-λ)\overrightarrow{AB}+\frac{λ}{2}\overrightarrow{AC}$;
同理由C,P,F三点共线得,$\overrightarrow{AP}=(1-μ)\overrightarrow{AC}+\frac{μ}{3}\overrightarrow{AB}$;
∴$\left\{\begin{array}{l}{1-λ=\frac{μ}{3}}\\{\frac{λ}{2}=1-μ}\end{array}\right.$;
解得$\left\{\begin{array}{l}{λ=\frac{4}{5}}\\{μ=\frac{3}{5}}\end{array}\right.$;
∴$\overrightarrow{BP}=\frac{4}{5}\overrightarrow{BE}=\frac{4}{5}(\frac{1}{2}\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{2}{5}\overrightarrow{AC}-\frac{4}{5}\overrightarrow{AB}$=$-\frac{4}{5}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b}$;
$\overrightarrow{CP}=\overrightarrow{BP}-\overrightarrow{BC}=\overrightarrow{BP}-\overrightarrow{AC}+\overrightarrow{AB}$=$\frac{2}{5}\overrightarrow{AC}-\frac{4}{5}\overrightarrow{AB}$$-\overrightarrow{AC}+\overrightarrow{AB}$=$\frac{1}{5}\overrightarrow{AB}-\frac{3}{5}\overrightarrow{AC}$=$\frac{1}{5}\overrightarrow{a}-\frac{3}{5}\overrightarrow{b}$;
(2)设$\overrightarrow{BD}=x\overrightarrow{BC}=x(\overrightarrow{b}-\overrightarrow{a})$;
∴$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=(1-x)\overrightarrow{a}+x\overrightarrow{b}$;
∵$\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{BP}=\overrightarrow{a}+(-\frac{4}{5}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b})$=$\frac{1}{5}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b}$;
A,P,D三点共线,∴$\overrightarrow{AP}$∥$\overrightarrow{AD}$;
∴存在k,使得$\overrightarrow{AD}=k\overrightarrow{AP}$=$\frac{k}{5}\overrightarrow{a}+\frac{2k}{5}\overrightarrow{b}$;
∴$\left\{\begin{array}{l}{1-x=\frac{k}{5}}\\{x=\frac{2k}{5}}\end{array}\right.$;
解得$\left\{\begin{array}{l}{k=\frac{5}{3}}\\{x=\frac{2}{3}}\end{array}\right.$;
∴$\overrightarrow{BD}=\frac{2}{3}\overrightarrow{BC}$;
∴$\frac{BD}{DC}=2$.
点评 考查共线向量基本定理,平面向量基本定理,向量加法、减法,及数乘的几何意义,以及向量的数乘运算.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a|>|b| | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | a2>b2 | D. | 2a>2b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
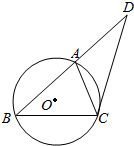 如图,圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,若AD=4,CD=6,则AC的长为( )
如图,圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,若AD=4,CD=6,则AC的长为( )| A. | 5 | B. | 4 | C. | $\frac{10}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
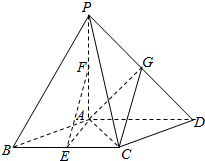 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点E,F,G分别为BC,PA,PD的中点,且PA=AB=2.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点E,F,G分别为BC,PA,PD的中点,且PA=AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com