
【题目】给定椭圆![]()
![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
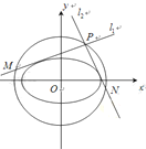
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的动点,过点
的“准圆”上的动点,过点![]() 作椭圆的切线
作椭圆的切线![]() 交“准圆”于点
交“准圆”于点![]() .
.
①当点![]() 为“准圆”与
为“准圆”与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 的方程并证明
的方程并证明![]() ;
;
②求证:线段![]() 的长为定值.
的长为定值.
【答案】(1)椭圆方程为![]() ,准圆方程为
,准圆方程为![]() ;(2)①
;(2)①![]() ,证明见解析;②证明见解析
,证明见解析;②证明见解析
【解析】
(1)根据题意![]() ,得到椭圆方程和准圆方程.
,得到椭圆方程和准圆方程.
(2)(ⅰ)设直线为![]() ,联立方程计算
,联立方程计算![]() 得到
得到![]() ,得到答案.
,得到答案.
(ⅱ)考虑斜率存在和不存在两种情况,设点![]() ,切线为
,切线为![]() ,联立方程得到
,联立方程得到![]() ,
,![]() ,得到直线
,得到直线![]() 垂直,得到线段
垂直,得到线段![]() 为准圆的直径,得到答案.
为准圆的直径,得到答案.
(1)![]() ,
,![]() 椭圆方程为
椭圆方程为![]() ,准圆方程为
,准圆方程为![]() .
.
(2)(ⅰ)因为准圆![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,
,
设过点![]() 且与椭圆相切的直线为
且与椭圆相切的直线为![]() ,
,
所以由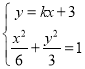 得
得![]() .
.
因为直线![]() 与椭圆相切,所以
与椭圆相切,所以![]() ,解得
,解得![]() ,
,
所以![]() 方程为
方程为![]() ,
,![]() ,
,![]() .
.
(ⅱ)①当直线![]() 中有一条斜率不存在时,不妨设直线
中有一条斜率不存在时,不妨设直线![]() 斜率不存在,
斜率不存在,
则![]() :
:![]() ,当
,当![]() :
:![]() 时,
时,![]() 与准圆交于点
与准圆交于点![]() ,
,
此时![]() 为
为![]() (或
(或![]() ),显然直线
),显然直线![]() 垂直;
垂直;
同理可证当![]() :
:![]() 时,直线
时,直线![]() 垂直
垂直
②当![]() 斜率存在时,设点
斜率存在时,设点![]() ,其中
,其中![]() .
.
设经过点![]() 与椭圆相切的直线为
与椭圆相切的直线为![]() ,
,
所以由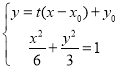 得
得![]() .
.
由![]() 化简整理得
化简整理得![]() ,
,
因为![]() ,所以有
,所以有![]() .
.
设![]() 的斜率分别为
的斜率分别为![]() ,因为
,因为![]() 与椭圆相切,
与椭圆相切,
所以![]() 满足上述方程
满足上述方程![]() ,
,
所以![]() ,即
,即![]() 垂直.
垂直.
综合①②知:因为![]() 经过点
经过点![]() ,又分别交其准圆于点
,又分别交其准圆于点![]() ,且
,且![]() 垂直.
垂直.
所以线段![]() 为准圆
为准圆![]() 的直径,
的直径,![]() ,
,
所以线段![]() 的长为定值6.
的长为定值6.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在![]() 岁之间的200人进行调查,并按年龄绘制出频率分布直方图,如图.
岁之间的200人进行调查,并按年龄绘制出频率分布直方图,如图.
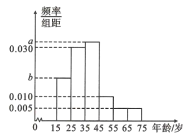
若把年龄在区间![]() ,
,![]() 内的人分别称为“青少年”“中老年”.经统计“青少年”和“中老年”的人数之比为
内的人分别称为“青少年”“中老年”.经统计“青少年”和“中老年”的人数之比为![]() .其中“青少年”中有40人关注“两会”,“中老年”中关注“两会”和不关注“两会”的人数之比为
.其中“青少年”中有40人关注“两会”,“中老年”中关注“两会”和不关注“两会”的人数之比为![]() .
.
(1)求图中![]() 的值.
的值.
(2)现采用分层抽样在![]() 和
和![]() 中随机抽取8人作为代表,从8人中任选2人,求2人都是“中老年”的概率.
中随机抽取8人作为代表,从8人中任选2人,求2人都是“中老年”的概率.
(3)根据已知条件,完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() %的把握认为“中老年”比“青少年”更加关注“两会”.
%的把握认为“中老年”比“青少年”更加关注“两会”.
关注 | 不关注 | 总计 | |
“青少年” | |||
“中老年” | |||
总计 |
附: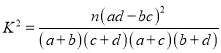 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x+b|,ab>0.
(1)当a=1,b=1时,求不等式f(x)<3的解集;
(2)若f(x)的最小值为2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.


由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学长期坚持贯彻以人为本,因材施教的教育理念,每年都会在校文化节期间举行“数学素养能力测试”和“语文素养能力测试”两项测试,以给学生课外兴趣学习及辅导提供参考依据.成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级(等级
五个等级(等级![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别对应5分,4分,3分,2分,1分).某班学生两科的考试成绩的数据统计如图所示,其中“语文素养能力测试”科目的成绩为
分别对应5分,4分,3分,2分,1分).某班学生两科的考试成绩的数据统计如图所示,其中“语文素养能力测试”科目的成绩为![]() 的考生有3人.
的考生有3人.
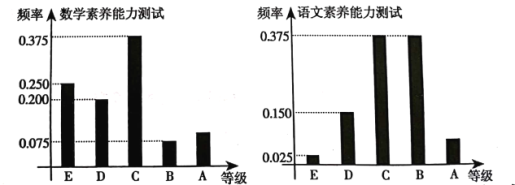
(1)求该班“数学素养能力测试”的科目平均分以及“数学素养能力测试”科目成绩为![]() 的人数;
的人数;
(2)若该班共有9人得分大于7分,其中有2人10分,3人9分,4人8分.从这9人中随机抽取三人,设三人的成绩之和为![]() ,求
,求![]() .
.
(3)从该班得分大于7分的9人中选3人即甲,乙,丙组队参加学校内的“数学限时解题挑战赛”.规则为:每队首先派一名队员参加挑战赛,在限定的时间,若该生解决问题,即团队挑战成功,结束挑战;若解决问题失败,则派另外一名队员上去挑战,直至派完队员为止.通过训练,已知甲,乙,丙通过挑战赛的概率分别是![]() ,
,![]() ,
,![]() ,问以怎样的先后顺序派出队员,可使得派出队员数目的均值达到最小?(只需写出结果)
,问以怎样的先后顺序派出队员,可使得派出队员数目的均值达到最小?(只需写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]()
(Ⅰ)求数列![]() 的通项
的通项![]() ,及前
,及前![]() 项和
项和![]()
(Ⅱ)请你在数列![]() 的前4项中选出三项,组成公比的绝对值小于1的等比数列
的前4项中选出三项,组成公比的绝对值小于1的等比数列![]() 的前3项,并记数列
的前3项,并记数列![]() 的前n项和为
的前n项和为![]() .若对任意正整数
.若对任意正整数![]() ,不等式
,不等式![]() 恒成立,试求
恒成立,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的标准方程是
的标准方程是![]() ,设
,设![]() 是椭圆
是椭圆![]() 的左焦点,
的左焦点,![]() 为直线
为直线![]() 上任意一点,过
上任意一点,过![]() 做
做![]() 的垂线交椭圆
的垂线交椭圆![]() 于点
于点![]() ,
,![]() .
.
(1)证明:线段![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(2)当![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为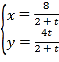 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() (
(![]() )与直线
)与直线![]() 和曲线
和曲线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com