
分析 (Ⅰ)利用椭圆C短轴的一个端点与长轴的一个端点的连线与圆O:x2+y2=$\frac{4}{3}$相切,推出$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}=\frac{4}{3}$,以及c=$\sqrt{2}$,然后求解椭圆方程.
(Ⅱ)①当直线l的斜率不存在时,求出A、B、P、Q坐标,然后求解S△ABQ.
②当直线l的斜率存在时,设其方程设为y=kx+m,设A(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=kx+m}\end{array}\right.$,消去y利用韦达定理判别式以及弦长公式,点到直线的距离,求出S△ABQ=$\frac{1}{2}$|PQ||AB利用基本不等式求解最值,然后推出结果.
解答 解:(Ⅰ)因为椭圆C短轴的一个端点与长轴的一个端点的连线与圆O:x2+y2=$\frac{4}{3}$相切,
所以$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}=\frac{4}{3}$,…(1分)
又抛物线y2=-4$\sqrt{2}x$其准线方程为x=$\sqrt{2}$,
因为抛物线y2=-4$\sqrt{2}x$的准线恰好过椭圆C的一个焦点,
所以c=$\sqrt{2}$,从而a2-b2=c2=2 …(2分)
两式联立,解得b2=2,a2=4,
所以椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$ …(4分)
①当直线l的斜率不存在时,不妨设直线AB方程为l:x=$\frac{2\sqrt{3}}{3}$,
则A($\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$),B($\frac{2\sqrt{3}}{3}$,-$\frac{2\sqrt{3}}{3}$),P($\frac{2\sqrt{3}}{3}$,0),所以Q(-$\frac{2\sqrt{3}}{3}$,0),
从而S△ABQ=$\frac{1}{2}$|PQ||AB|=$\frac{1}{2}×\frac{4\sqrt{3}}{3}×\frac{4\sqrt{3}}{3}$=$\frac{8}{3}$ …(5分)
②当直线l的斜率存在时,设其方程设为y=kx+m,设A(x1,y1),B(x2,y2),
联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=kx+m}\end{array}\right.$,消去y得(1+2k2)x2+4kmx+2m2-4=0,
△=(4mk)2-4(2k2+1)(2m2-4)=8(4k2-m2+2)>0,
即4k2-m2+2>0
$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{4km}{1+2{k}^{2}}}\\{{x}_{1}{x}_{2}=\frac{2({m}^{2}-2)}{1+2{k}^{2}}}\end{array}\right.$ …(6分)
因为直线与圆相切,所以d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{\frac{4}{3}}$,∴3m2=4(1+k2) …(7分)
|AB|=$\sqrt{(1+{k}^{2})({{x}_{1}-{x}_{2})}^{2}}$=$\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\frac{4\sqrt{3}}{3}$$\sqrt{\frac{{k}^{4}+5{k}^{2}+1}{(1+2{k}^{2})^{2}}}$
=$\frac{4\sqrt{3}}{3}$$\sqrt{1+\frac{{k}^{2}}{4{k}^{4}+4{k}^{2}+1}}$ …(8分)
当k≠0时,|AB|=$\frac{4\sqrt{3}}{3}$$\sqrt{1+\frac{{k}^{2}}{4{k}^{4}+4{k}^{2}+1}}$=$\frac{4\sqrt{3}}{3}×\sqrt{1+\frac{1}{4{k}^{2}+\frac{1}{{k}^{2}}+4}}$,
因为4k2+$\frac{1}{{k}^{2}}+4≥8$,
所以1<1+$\frac{1}{4{k}^{2}+\frac{1}{{k}^{2}}+4}$$≤\frac{9}{8}$,所以$\frac{4\sqrt{3}}{3}<|AB|≤\sqrt{6}$.…(9分)
因为PQ圆O的直径,所以S△ABQ=$\frac{1}{2}$|PQ||AB|=$\frac{1}{2}×\frac{4\sqrt{3}}{3}×|AB|$=$\frac{2\sqrt{3}}{3}|AB|$.…(10分)
所以$\frac{8}{3}$<S△ABQ≤2$\sqrt{2}$.…(11分)
k=0时,S△ABQ=$\frac{1}{2}$|PQ||AB|=$\frac{1}{2}$×$\frac{4\sqrt{3}}{3}$×$\frac{4\sqrt{3}}{3}$=$\frac{8}{3}$
综上可得△ABQ面积的取值范围为[$\frac{8}{3}$,2$\sqrt{2}$].…(12分)
点评 本题考查椭圆方程的求法,抛物线以及椭圆的位置关系的综合应用,考查转化思想以及计算能力.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{14}{15}$ | B. | $\frac{13}{15}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0} | C. | {1} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
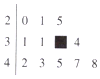 在如图所示一组数据的茎叶图中,有一个数字被污染后而模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )
在如图所示一组数据的茎叶图中,有一个数字被污染后而模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com