
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 对于①,先根据定义域选择解析式来构造不等式,当0≤x≤1时,由2(1-x)≤x求解;当1<x≤2时,由x-1≤x求解,取后两个结果取并集;
对于②,先求得f(0),f(1),f(2),再分别求得f(f(0)),f(f(f(0)));f(f(1)),f(f(f(1)));f(f(f(2))).再观察与自变量是否相等即可;
对于③,看问题有2016,2017求值,一定用到周期性,所以先求出几个,观察是以4为周期,求解即可;
对于④,结合①②③可得$\frac{2}{3}$、0、1、2、$\frac{8}{9}$、$\frac{2}{9}$、$\frac{14}{9}$、$\frac{5}{9}$∈M,进而可得结论.
解答 解:当0≤x<1时,f(x)=2(1-x);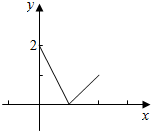
当1≤x≤2时,f(x)=x-1.
即有f(x)=$\left\{\begin{array}{l}{2(1-x),0≤x<1}\\{x-1,1≤x≤2}\end{array}\right.$,
画出y=f(x)在[0,2]的图象.
对于①,可得f(x)≤x,当1≤x≤2时,x-1≤x成立;
当0≤x<1时,2(1-x)≤x,解得$\frac{2}{3}$≤x<1,即有定义域为{x|$\frac{2}{3}$≤x≤2},
故①正确;
对于②,当x=0时,f3(0)=f[f2(0)]=f(f(f(0)))=f(f(2))=f(1)=0成立;
当x=1时,f3(1)=f[f2(1)]=f(f(f(1)))=f(f(0))=f(2)=1成立;
当x=2时,f3(2)=f[f2(2)]=f(f(f(2)))=f(f(1))=f(0)=2成立;
即有A=B,故②正确;
对于③,f1($\frac{8}{9}$)=2(1-$\frac{8}{9}$)=$\frac{2}{9}$,f2($\frac{8}{9}$)=f(f($\frac{8}{9}$))=f($\frac{2}{9}$)=2(1-$\frac{2}{9}$)=$\frac{14}{9}$,
f3($\frac{8}{9}$)=f(f2($\frac{8}{9}$))=f($\frac{14}{9}$)=$\frac{14}{9}$-1=$\frac{5}{9}$,f4($\frac{8}{9}$)=f(f3($\frac{8}{9}$))=f($\frac{5}{9}$)=2(1-$\frac{5}{9}$)=$\frac{8}{9}$,
一般地,f4k+r($\frac{8}{9}$)=fr($\frac{8}{9}$)(k,r∈N).
即有f2016($\frac{8}{9}$)+f2017($\frac{8}{9}$)=f4($\frac{8}{9}$)+f1($\frac{8}{9}$)=$\frac{8}{9}$+$\frac{2}{9}$=$\frac{10}{9}$,故③不正确;
对于④,由(1)知,f($\frac{2}{3}$)=$\frac{2}{3}$,∴fn($\frac{2}{3}$)=$\frac{2}{3}$,则f12($\frac{2}{3}$)=$\frac{2}{3}$,∴$\frac{2}{3}$∈M.
由(2)知,对x=0、1、2,恒有f3(x)=x,∴f12(x)=x,则0、1、2∈M.
由(3)知,对x=$\frac{8}{9}$、$\frac{2}{9}$、$\frac{14}{9}$、$\frac{5}{9}$,恒有f12(x)=x,∴$\frac{8}{9}$、$\frac{2}{9}$、$\frac{14}{9}$、$\frac{5}{9}$∈M.
综上所述$\frac{2}{3}$、0、1、2、$\frac{8}{9}$、$\frac{2}{9}$、$\frac{14}{9}$、$\frac{5}{9}$∈M.
∴M中至少含有8个元素.故④正确.
故选:C.
点评 本题考查的知识点是分段函数及分段不等式的解法,元素与集合关系的判定,函数的周期性,函数恒成立问题,分段函数问题要注意分类讨论,还考查了分段函数多重求值,要注意从内到外,根据自变量取值选择好解析式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
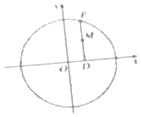 如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.
如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{5π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
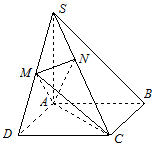 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.05 |
| [60,70) | a | 0.20 |
| [70,80) | 35 | b |
| [80,90) | 25 | 0.25 |
| [90,100) | 15 | 0.15 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既有极大值,也有极小值 | B. | 有极大值,没有极小值 | ||
| C. | 没有极大值,有极小值 | D. | 既无极大值,也没有极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com