
在空间直角坐标系O-xyz中有8个点:P1(1,1,1)、P2(-1,1,1)、…、P7(-1,-1,-1)、P8(1,-1,-1)(每个点的横、纵、竖坐标都是1或-1),以其中4个点为顶点的三棱锥一共有________个(用数字作答).
科目:高中数学 来源: 题型:
甲和乙等五名志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
A.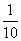 B.
B.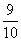
C.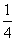 D.
D.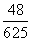
查看答案和解析>>
科目:高中数学 来源: 题型:
设平面向量am=(m,1),bn=(2,n),其中m、n∈{1,2,3,4}.
(1)请列出有序数组(m,n)的所有可能结果;
(2)记“使得am⊥(am-bn)成立的(m,n)”为事件A,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
10名同学合影,站成了前排3人,后排7人.现摄影师要从后排7人中抽2个站前排,其他人的相对顺序不变,则不同调整方法的种数为( )
A.C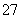 A
A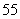 B.C
B.C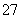 A
A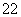
C.C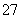 A
A D.C
D.C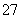 A
A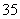
查看答案和解析>>
科目:高中数学 来源: 题型:
某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.

(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)

乙的频数统计表(部分)
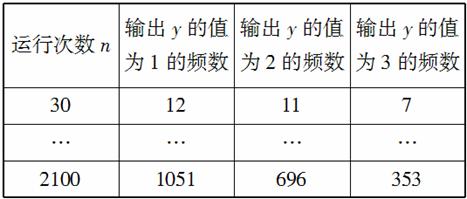
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;
(3)将按程序框图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com