练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f(x)＝x2－bx＋3.

    (1)若f(0)＝f(4)，求函数f(x)的零点；

    (2)若函数f(x)一个零点大于1，另一个零点小于1，求b的取值范围．

    【答案】（1）1和3 (2) b的取值范围为(4，＋∞)

    【解析】试题分析：（1）由，得出，再将代入函数，解方程即可；（2）根据二次函数的图象，只需即可.

    试题解析：(1)由f(0)＝f(4)，得3＝16－4b＋3，即b＝4，所以f(x)＝x2－4x＋3，令f(x)＝0，

    即x2－4x＋3＝0，得x1＝3，x2＝1，

    所以f(x)的零点是1和3.

    (2)因为f(x)的零点一个大于1，另一个小于1，如图．

    需f(1)<0，即1－b＋3<0，所以b>4.

    故b的取值范围为(4，＋∞)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】以下是新兵训练时，某炮兵连8周中炮弹对同一目标的命中情况的柱状图：

    （1）计算该炮兵连这8周中总的命中频率，并确定第几周的命中频率最高；

    （2）以（1）中的作为该炮兵连炮兵甲对同一目标的命中率，若每次发射相互独立，且炮兵甲发射3次，记命中的次数为，求的数学期望；

    （3）以（1）中的作为该炮兵连炮兵对同一目标的命中率，试问至少要用多少枚这样的炮弹同时对该目标发射一次，才能使目标被击中的概率超过？（取）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市居民用水原价为2.25元/立方米，从2010年1月1日起实行阶梯式计价：

    级数

    计算水费的用水量/立方米

    单价/(元/立方米)

    1

    不超过20立方米

    1.8

    2

    超过20立方米至30立方米

    2.4

    3

    超过30立方米

    p

    其中p是用水总量的一次函数，已知用水总量为40立方米时p＝3.0元/立方米，用水总量为50立方米时p＝3.5元/立方米．

    (1)写出水价调整后居民每月水费额与用水量的函数关系式．每月用水量在什么范围内，水价调整后居民同等用水的水费比调整前增加？

    (2)用一个流程图描述水价调整后计算水费的主要步骤．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求函数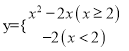的值的程序框图如图所示.

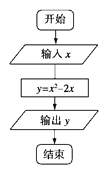
    (1)指出程序框图中的错误，并写出算法；

    (2)重新绘制解决该问题的程序框图，并回答下面提出的问题．

    ①要使输出的值为正数，输入的x的值应满足什么条件？

    ②要使输出的值为8，输入的x值应是多少？

    ③要使输出的y值最小，输入的x值应是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设， .

    （1）若，证明： 时， 成立；

    （2）讨论函数的单调性；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

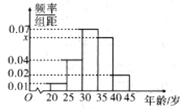
    【题目】为创建全国文明城市，某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名，按年龄作分组如下：[20,25) , [25,30) , [30,35)， [35,40) , [40,45] ，并得到如下频率分布直方图.

    (Ⅰ)求图中 的值，并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数；

    (Ⅱ)在抽取的100名志愿者中按年龄分层抽取10名参加区电视台“文明伴你行”节目录制，再从这10名志愿者中随机选取3名到现场分享劝导制止行人闯红灯的经历，记这3名志愿者中年龄不低于35岁的人数为 ,求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经过下列两点的直线的斜率是否存在？如果存在，求其斜率，并确定直线的倾斜角α.

    (1)A(2,3)，B(4,5)；

    (2)C(－2,3)，D(2，－1)；

    (3)P(－3,1)，Q(－3,10)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的图象过点。

    （1）求的值并求函数的值域；

    （2）若关于的方程有实根，求实数的取值范围；

    （3）若函数， ，则是否存在实数，使得函数的最大值为0？若存在，求出的值；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线与函数的图像相切于点．

    （1）求实数的值；

    （2）证明除切点外，直线总在函数的图像的上方；

    （3）设是两两不相等的正实数，且成等比数列，试判断与的大小关系，并证明你的结论．

    查看答案和解析>>

    同步练习册答案