
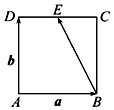
| A. | $\frac{1}{2}$$\vec b$+$\vec a$ | B. | $\vec b$$-\frac{1}{2}$$\vec a$ | C. | $\frac{1}{2}$$\vec a$+$\vec b$ | D. | $\vec a$-$\frac{1}{2}$$\vec b$ |
分析 利用向量的加、减法法则将$\overrightarrow{BE}$用基向量$\overrightarrow{AB}$,$\overrightarrow{AD}$表示出即可.
解答 解:∵四边形ABCD为正方形,E为CD边的中点,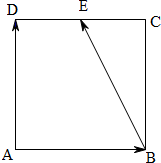
∴2$\overrightarrow{BE}$=$\overrightarrow{BD}$+$\overrightarrow{BC}$=$\overrightarrow{BA}$+$\overrightarrow{AD}$+$\overrightarrow{BC}$,
在正方形ABCD中,$\overrightarrow{BC}$=$\overrightarrow{AD}$,
又∵$\overrightarrow{BA}$=-$\overrightarrow{AB}$,
∴2$\overrightarrow{BE}$=-$\overrightarrow{AB}$+2$\overrightarrow{AD}$=2$\overrightarrow{b}$-$\overrightarrow{a}$,
∴$\overrightarrow{BE}$=$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$,
故选:B.
点评 本题考查了向量的加法原理与向量的减法原理,以及平面向量基本定理.解题的关键是运用向量加法和减法的三角形法则或平行四边形法则,将要求的向量一步一步向已知的向量转化.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x^2}$ | B. | $y=\root{3}{x^3}$ | C. | $y={(\sqrt{x})^2}$ | D. | $y=\frac{x^2}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
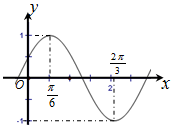 已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )| A. | 1,2,-$\frac{π}{3}$ | B. | 1,$\frac{1}{2}$,-$\frac{π}{3}$ | C. | 1,2,$\frac{π}{6}$ | D. | 1,$\frac{1}{2}$,$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | (5,+∞) | C. | $(1,\frac{5}{2})$ | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com