解:(1)f'(x)=
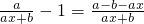
充分性:因为x≥0,a>0,b>0所以,当f'(x)≤0时,a-b≤0,即a≤b
必要性:当a≤b时,因为a>0,b>0,x≥0,所以ax+b>0,a-b-ax≤0,即f'(x)≤0
所以f(x)在[0,+∝)上是减函数的充要条件是“a≤b”
(2)由(1)知当a≤b时f(x)在[0,+∝)上是减函数
∴f(x)的最大值为f(0)=lnb
当b<a时,因为f'(x)=
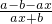
∴当0≤x<

时,f'(x)>0;当x>

时,f'(x)<0
即f(x)在[0,

]是增函数,f(x)在[

,+∞]是减函数
则当x=

时取得最大值为lna-

综上,[f(x)max]=
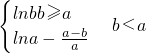
(3)在(1)中取a=b=1,得f(x)=ln(x+1)-x
由(1)知f(x)在[0,+∝)上是减函数
∵ln(1+
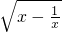
)-
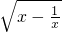
≤ln2-1即f(
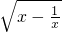
)≤f(1)
∴
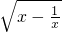
≥1解得

≤x<0或x≥

∴不等式的解集为[

,0)∪[

,+∞
分析:(1)先求出函数的导数,再求充分性由x≥0,a>0,b>0?当f'(x)≤0时,a-b≤0;然后求必要性:当a≤b时,由a>0,b>0,x≥0,?ax+b>0,a-b-ax≤0,即可求出充要条件;
(2)由(1)能够得出当a≤b时,(x)的最大值为f(0)=lnb;当b<a时,f(x)在[0,

]是增函数,f(x)在[

,+∞]是减函数,进而求得当x=

时取得最大值为lna-

,最后在总结即可;
(3)解不等式ln(1+
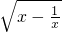
)-
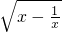
≤ln2-1能够转化成f(
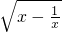
)≤f(1),再根据函数的单调性即可求出解题.
点评:本题考查了函数单调性和导数的关系以及利用导数求出最值,第(2)要注意分情况求最值,属于中档题.

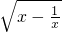 )-
)-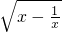 ≤ln2-1.
≤ln2-1.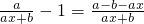
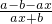
 时,f'(x)>0;当x>
时,f'(x)>0;当x> 时,f'(x)<0
时,f'(x)<0 ]是增函数,f(x)在[
]是增函数,f(x)在[ ,+∞]是减函数
,+∞]是减函数 时取得最大值为lna-
时取得最大值为lna-
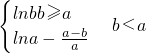
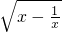 )-
)-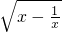 ≤ln2-1即f(
≤ln2-1即f(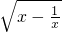 )≤f(1)
)≤f(1)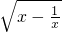 ≥1解得
≥1解得 ≤x<0或x≥
≤x<0或x≥
 ,0)∪[
,0)∪[ ,+∞
,+∞ ]是增函数,f(x)在[
]是增函数,f(x)在[ ,+∞]是减函数,进而求得当x=
,+∞]是减函数,进而求得当x= 时取得最大值为lna-
时取得最大值为lna- ,最后在总结即可;
,最后在总结即可;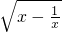 )-
)-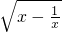 ≤ln2-1能够转化成f(
≤ln2-1能够转化成f(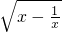 )≤f(1),再根据函数的单调性即可求出解题.
)≤f(1),再根据函数的单调性即可求出解题.
