
分析 (1)数列{an}是公差为2的等差数列,a1,a4,a13成等比数列,d=2${({a_1}+3d)^2}={a_1}({a_1}+12d)$求得a1,根据等差数列通项公式即可求得an,由$\frac{b_n}{a_n}={3^{n-1}}$,将an,的通项公式代入即可求得数列{bn}的通项公式;
(2)由(1)可知,利用乘以公比“错位相减法”求得数列{bn}前n项和,求得数列{an}的前n项和,即可求得Rn,根据式$\frac{{R}_{n}}{n}$≤λ•3n+n+3,采用分离变量$λ≥1-\frac{1}{3^n}$,根据函数的单调性,求λ的取值范围.
解答 解:(1)依题意得d=2${({a_1}+3d)^2}={a_1}({a_1}+12d)$…(2分)
解得a1=3…(3分)
∴an=a1+(n-1)d=3+2(n-1)=2n+1,即an=2n+1. …(4分)
又数列$\left\{{\frac{b_n}{a_n}}\right\}$是首项为1,公比为3的等比数列,
∴$\frac{b_n}{a_n}={3^{n-1}}$,
∴${b_n}={a_n}•{3^{n-1}}=(2n+1)•{3^{n-1}}$…(7分)
(2)令${T_n}=3+5•3+7•{3^2}+…+(2n+1)•{3^{n-1}}$,
$3{T_n}=\;3•3+5•{3^2}+7•{3^3}+…+(2n-1)•{3^{n-1}}+(2n+1)•{3^n}$,
两式相减得:$-2{T_n}=3+2•3+2•{3^2}+…+2•{3^{n-1}}-(2n+1){3^n}$,
$\begin{array}{l}=3+2•\frac{{3(1-{3^{n-1}})}}{1-3}-(2n+1){3^n}\\=-2n•{3^n}\end{array}$,
∴${T_n}=n•{3^n}$…(10分)
∴${R_n}=n•{3^n}+3+5+7+…+2n+1=n•{3^n}+\frac{(3+2n+1)n}{2}$,
=n(3n+n+2)…(12分)
由$\frac{R_n}{n}≤λ•{3^n}+n+3$对n∈N+恒成立可得$λ≥1-\frac{1}{3^n}$对n∈N+恒成立,
则λ≥1…(15分)
点评 本题考查求数列的通项公式及等差数列前n项和公式,主要考察采用“错位相减法”求数列的前n项和,分离变量法求未知数的取值范围,考察学生分析问题解决问题的能力,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 5 | 6 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
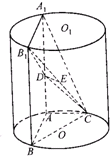 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,3\sqrt{5})$ | B. | $[-\sqrt{5},\sqrt{5}]$ | C. | $(-3\sqrt{5},3\sqrt{5})$ | D. | $(0,\sqrt{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$>1 | B. | a2>b2 | C. | (${\frac{1}{2}}$)a<(${\frac{1}{2}}$)b | D. | lg(a-b)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果a>b,那么ac2>bc2 | B. | 如果a>b,那么a2>b2 | ||
| C. | 如果a>b,ab>0,那么$\frac{1}{a}<\frac{1}{b}$ | D. | 如果x≠0,那么$x+\frac{1}{x}≥2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com