
分析 将行列式$|\begin{array}{l}{1}&{x}&{{x}^{2}}\\{1}&{2}&{4}\\{1}&{3}&{9}\end{array}|$展开,整理得$|\begin{array}{l}{1}&{x}&{{x}^{2}}\\{1}&{2}&{4}\\{1}&{3}&{9}\end{array}|$=x2-5x+6,由x2-5x+6=0,即可求得x的值.
解答 解:$|\begin{array}{l}{1}&{x}&{{x}^{2}}\\{1}&{2}&{4}\\{1}&{3}&{9}\end{array}|$=1×2×9+x×4×1+1×3×x2-2×1×x2-1×9×x-1×3×4=x2-5x+6,
∴x2-5x+6=0,解得:x=2或x=3,
故答案为:x=2或x=3.
点评 本题考查三阶矩阵的展开,考查一元二次方程的解,考查计算能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
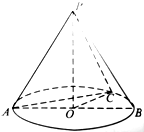 如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$的中点,则二面角B-PA-C的余弦值为( )
如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$的中点,则二面角B-PA-C的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{15}}{5}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
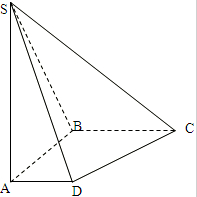 如图,ABCD是直角梯形,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=2,AD=1,求面SCD与面SBA所成二面角的大小.
如图,ABCD是直角梯形,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=2,AD=1,求面SCD与面SBA所成二面角的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
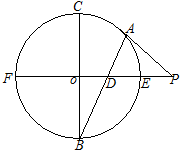 如图,直线PA为⊙O的切线,切点为A,PO交⊙O于E,F两点,直径BC⊥OP,连接AB交PO于点D.
如图,直线PA为⊙O的切线,切点为A,PO交⊙O于E,F两点,直径BC⊥OP,连接AB交PO于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com