
分析 设圆内接等腰三角形ABC的底边长为2x,高为h.运用勾股定理可得x=$\sqrt{h(4-h)}$,进而得到面积函数的解析式,求出导数,单调区间,可得h=3处取得极大值,且为最大值.
解答 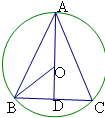 解 设圆内接等腰三角形ABC的底边长为2x,高为h.
解 设圆内接等腰三角形ABC的底边长为2x,高为h.
那么h=AO+OD=2+$\sqrt{4-{x}^{2}}$,解得x2=h(4-h),
于是内接三角形的面积为S=x•h=$\sqrt{h(4-h)}$•h,
由S′=$\frac{h(2-h)}{\sqrt{h(4-h)}}$+$\sqrt{h(4-h)}$=$\frac{2h(3-h)}{\sqrt{h(4-h)}}$,(0<h<4).
令S′=0,解得h=3,
当h∈(0,3)时,S′>0,函数S递增;
当h∈(3,4)时,S′<0,函数S递减.
可得函数S在h=3处取得极大值,且为最大值.
故答案为:3.
点评 本题考查导数在实际问题中的运用:求最值,正确求出面积函数的解析式,并求出导数是解题的关键,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD是边长为2的为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹的长度为( )
如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD是边长为2的为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹的长度为( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | π | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正三棱柱ABC-A1B1C1的所有棱长都相等,D,E分别是AB,BB1的中点.
正三棱柱ABC-A1B1C1的所有棱长都相等,D,E分别是AB,BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com