
分析 (1)直线l的极坐标方程$ρsin(θ+\frac{π}{4})$=2$\sqrt{2}(m+1)$,展开化为$\frac{\sqrt{2}}{2}$(ρsinθ+ρcosθ)=2$\sqrt{2}$(m+1),利用互化公式可得直角坐标方程.而曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{2}cosφ}\\{y=\sqrt{2}sinφ}\end{array}\right.$(其中φ为参数),利用平方关系消去参数可得普通方程.利用点到直线的距离公式、直线与圆相切的充要条件即可得出.
(2)m=-$\frac{3}{4}$时,圆心到直线l的距离d=$\frac{\sqrt{2}}{2}$,利用弦长公式可得:直线l被曲线C截得的弦长=2$\sqrt{{r}^{2}-{d}^{2}}$.
解答 解:(1)直线l的极坐标方程$ρsin(θ+\frac{π}{4})$=2$\sqrt{2}(m+1)$,展开化为$\frac{\sqrt{2}}{2}$(ρsinθ+ρcosθ)=2$\sqrt{2}$(m+1),即x+y-4(m+1)=0.
而曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{2}cosφ}\\{y=\sqrt{2}sinφ}\end{array}\right.$(其中φ为参数),消去参数可得:x2+y2=2.
∵直线l与曲线C恰好有一个公共点,∴$\frac{4|m+1|}{\sqrt{2}}$=$\sqrt{2}$.
∴m+1=$±\frac{1}{2}$,解得m=$-\frac{1}{2}$,或$-\frac{3}{2}$.
(2)m=-$\frac{3}{4}$时,圆心到直线l的距离d=$\frac{4|m+1|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
∴直线l被曲线C截得的弦长=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{2-(\frac{\sqrt{2}}{2})^{2}}$=$\sqrt{6}$.
点评 本题考查了参数方程化为普通方程、极坐标与直角坐标的互化、直线与圆相交弦长公式、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
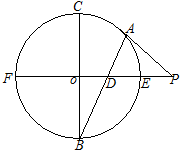 如图,直线PA为⊙O的切线,切点为A,PO交⊙O于E,F两点,直径BC⊥OP,连接AB交PO于点D.
如图,直线PA为⊙O的切线,切点为A,PO交⊙O于E,F两点,直径BC⊥OP,连接AB交PO于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 满意 | 24 | ||
| 不满意 | 6 | ||
| 总计 | 60 |
| P(K2≥k0) | 0.250 | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com